Question

17．如图1所示，已知正方形BCD的边长为1，点E为AB上一点，EF⊥EC，且EF=EC，连接AF．
（1）求∠EAF的度数；
（2）如图2所示，连接CF交BD于M，求证：M为CF的中点；
（3）如图2所示，当点E在正方形ABCD的边AB上运动时，式子AF+2DM的值是否会改变．若不变，请求出其值；若改变，请简述理由．

Answer 1

分析 （1）截取BG=BE，判断AE=GC，再判断出∠AEF=∠GCE，从而得到△AEF≌△GCE，即可；
（2）同（1）的方法得到△DMA≌△DMC判断出∠MFA=∠MAF，即MF=MA；
（3）先判断出四边形ABDH是平行四边形，再得出DM是△CFH的中位线，最后用勾股定理即可．

解答 解：（1）如图1，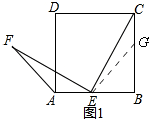

在BC上截取BG=BE，连接EG，
∵BG=BE，∠EBG=90°，
∴∠BGE=45°，∠CGE=135°，
∵AB=BC，BG=BE，
∴AE=GC，
∵EF⊥EC，
∴∠AEF+∠BEC=90°，
∵∠GCE+∠BEC=90°，
∴∠AEF=∠GCE，
在△AEF和△GCE中，
$\left\{\begin{array}{l}{AE=GC}\\{∠AEF=∠GCE}\\{EF=EC}\end{array}\right.$，
∴△AEF≌△GCE，
∴∠EAF=∠CGE=135°，
（2）如图2，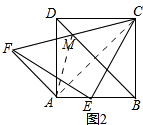

连接AM，AC
同（1）的方法，得，△DMA≌△DMC，
∴MA=MC，
∴∠MAC=∠MCA，
∵∠FAC=∠FAE-∠CAB=90°，
∴∠MFA+∠MCA=90°，
∵∠MAF+∠MAC=90°，
∴∠MFA=∠MAF，
∴MF=MA，
∴MF=MA=MC，
∴M是CF的中点；
（3）如图3，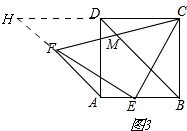

延长AF，CD交于H，
由（1）得，∠EAF=135°，
∴∠FAD=135°-90°=45°，
∵∠ADB=45°，
∴AH∥BD，
∵AB∥HD，
∴四边形ABDH是平行四边形，
∴DH=AB=CD，
∴D是CH中点，
∵M是CF中点，
∴DM是△CFH的中位线，
∴FH=2DM
在等腰Rt△HAD中，AH=$\sqrt{2}$AD，
∴AF+2DM=AF+FH=$\sqrt{2}$AD=$\sqrt{2}$．

点评 此题是四边形综合题，主要考查了正方形的性质，全等三角形的性质和判定，平行四边形的性质和判定，勾股定理，解本题的关键是构造全等三角形．