题目内容

13．若y=（x+2b）2-4b2+a2+3b和y=2（x-4）2-2b-1有相同的顶点，则a=5或-5，b=2．

分析 根据顶点坐标相同，可得方程组，根据解方程组，可得答案．

解答 解：由y=（x+2b）2-4b2+a2+3b和y=2（x-4）2-2b-1有相同的顶点，得
$\left\{\begin{array}{l}{-2b=4}\\{-4{b}^{2}+{a}^{2}+3b=-2b-1}\end{array}\right.$．
解得$\left\{\begin{array}{l}{a=5}\\{b=-2}\end{array}\right.$或$\left\{\begin{array}{l}{a=-5}\\{b=-2}\end{array}\right.$．
故答案为：5或-5，2．

点评 本题考查了二次函数的性质，利用顶点相同得出方程组是解题关键．

练习册系列答案
相关题目
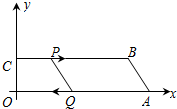17．如图，在直角坐标系中，四边形OABC的OA，OC两边分别在x，y轴上，OA∥BC，BC=15cm，A点坐标为（16，0），C点坐标为（0，4）．点P，Q分别从C，A同时出发，点P以2cm/s的速度由C向B运动，点Q以4cm/s的速度由A向O运动，当点Q到达点O时，点P也停止运动，设运动时间为t秒（0≤t≤4）．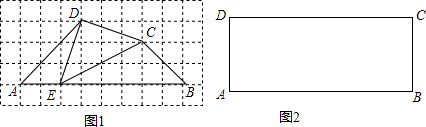
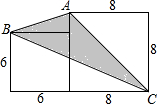（1）求当t为多少时？四边形PQAB为平行四边形；
（2）求当t为多少时？PQ所在直线将四边形OABC分成左右两部分的面积比为1：2；
（3）直接写出在（2）的情况下，直线PQ的函数关系式．
4．对于点E和四边形ABCD，给出如下定义：在四边形ABCD的边AB上任取一点E（点E不与A、B重合），分别连接ED、EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，则称E为四边形ABCD边AB上的“相似点”；如果这三个三角形都相似，我们称E为四边形ABCD边AB上的“强相似点”．
（1）如图1，在四边形ABCD中，A、B、C、D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，点E是AB边上一点，∠DEC=45°，试判断点E是否是四边形ABCD边AB上的相似点，并证明你的结论正确；
（2）如图2，在矩形ABCD中，AB=8，AD=3．
①在AB边上是否存在点E，使点E为四边形ABCD边AB上的“强相似点”．若存在，有几个？试在图2中画出所有强相似点；
②在①所画图形的基础上求AE的长．
1．如图，求阴影部分的面积．
8．作图题
（1）将△ABC向右平移4个单位长度，画出平移后的△A1B1C1；
（2）画出△ABC关于直线PQ对称的△A2B2C2；
（3）将△ABC绕原点O旋转180°，画出旋转后的△A3B3C3；
（4）在△A1B1C1、△A2B2C2、△A3B3C3中，△A1B1C1与△A3B3C3成中心对称．
18．如果半径分别为2和3的两圆外切，那么这两个圆的圆心距是（　　）
A．1B．5C．1或5D．大于1且小于5
5．先阅读，再解题．
解不等式：$\frac{3x+6}{x-2}$＞0．
解：根据两数相除，同号得正，异号得负，得
①$\left\{\begin{array}{l}{3x+6＞0}\\{x-2＞0}\end{array}\right.$或②$\left\{\begin{array}{l}{3x+6＜0}\\{x-2＜0}\end{array}\right.$
解不等式组①，得x＞2；
解不等式组②，得x＜-2．
所以原不等式的解集为x＞2或x＜-2．
参照以上解题过程所反映的解题方法，试解不等式：$\frac{2x-4}{5+3x}$＜0．
2．如图1点E、F是长方形纸带ABCD边上的两个点，∠DEF=20°，将这个纸带沿EF折叠成如图2的形状后，再沿BF折叠成图3的形状，则图3中的∠CFE的度数是120度．
3．下列由2和3组成的四个算式中，值最小的是（　　）
A．2-3B．2÷3C．23D．2-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网