题目内容
2．如图1点E、F是长方形纸带ABCD边上的两个点，∠DEF=20°，将这个纸带沿EF折叠成如图2的形状后，再沿BF折叠成图3的形状，则图3中的∠CFE的度数是120度．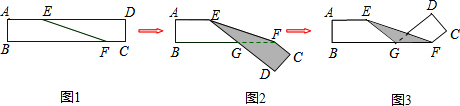
分析 先根据平行线的性质得出∠DEF=∠EFB，图2中根据图形折叠的性质得出∠AEF的度数，再由平行线的性质得出∠GFC=150°，图3中根据∠CFE=∠GFC-∠EFG即可得出结论．
解答 解：∵AD∥BC，
∴∠DEF=∠EFB=20°，
图2中，∠GFC=180°-2∠EFG=140°，
图3中，∠CFE=∠GFC-∠EFG=140°-20°=120°．
故答案为：120°．
点评 本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
14．汽车油箱中的余油量Q（升）与它行驶的时间t（小时）之间的关系如下表：
（1）求油箱中的余油量Q与行驶时间t的函数关系式；
（2）从开始算起，如果汽车每小时行驶40千米，当油箱中的油耗尽时，该汽车行驶了多少千米？
| 余油量Q/L | 60 | 50 | 40 | 30 | 20 | … |
| 行驶时间t/h | 0 | 2 | 4 | 6 | 8 | … |
（2）从开始算起，如果汽车每小时行驶40千米，当油箱中的油耗尽时，该汽车行驶了多少千米？
