题目内容
6.据报道,参加某次中俄海上联合军事演习的我国与俄罗斯共有超过4000名的官兵参加,参加此次军演的官兵如果增加128人,则恰好可以排成一个正方形方阵;如果减少128人,也恰好可以排成一个正方形方阵.请问此次参加军演的两国官兵共有多少人?分析 设此次参加军演的两国官兵共有x人,第1个正方形方阵的边长为m,第2个正方形方阵的边长为n,根据题意列出方程组,相减并利用平方差公式化简,由x的范围确定出m与n的值,进而求出x的值,即可得到结果.
解答 解:设此次参加军演的两国官兵共有x人,第1个正方形方阵的边长为m,第2个正方形方阵的边长为n,
根据题意得:$\left\{\begin{array}{l}{{m}^{2}=x+128}\\{{n}^{2}=x-128}\end{array}\right.$,
相减得:(m+n)(m-n)=256,
∵x>4000,∴$\left\{\begin{array}{l}{m+n=128}\\{m-2=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=65}\\{n=63}\end{array}\right.$,
∴x=652-128=4097.
则参加军演的官兵共有4097人.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
1.科研人员在测试一枚火箭竖直向上升空时发现,火箭的高度h(m)与时间t(s)的关系数据如下:
(1)根据上表,以时间t为横轴,高度h为纵轴建立直角坐标系,并描出上述各点;
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
| 时间t/s | 1 | 5 | 10 | 15 | 20 | 25 |
| 火箭高度h/m | 155 | 635 | 1010 | 1135 | 1010 | 635 |
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
 如图 在△ABC中,∠B=90° AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿边BC向C以4cm/s的速度移动. 如果P,Q分别从A,B同时出发 那么△PBQ的面积S随出发的时间t如何变化?写出函数关系式.并指出几秒后△PBQ的面积最大,最大面积是多少?
如图 在△ABC中,∠B=90° AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿边BC向C以4cm/s的速度移动. 如果P,Q分别从A,B同时出发 那么△PBQ的面积S随出发的时间t如何变化?写出函数关系式.并指出几秒后△PBQ的面积最大,最大面积是多少? 如图,在五边形ABCDE中,AB∥CD,∠A=125°,∠D=150°,求∠E的度数.
如图,在五边形ABCDE中,AB∥CD,∠A=125°,∠D=150°,求∠E的度数. 如图,在梯形ABCD中,CD∥AB,BE是∠ABC的平分线,BE⊥AD于E,且$\frac{DE}{AE}$=$\frac{1}{2}$,求$\frac{{S}_{△ABE}}{{S}_{四边形BCDE}}$的值.
如图,在梯形ABCD中,CD∥AB,BE是∠ABC的平分线,BE⊥AD于E,且$\frac{DE}{AE}$=$\frac{1}{2}$,求$\frac{{S}_{△ABE}}{{S}_{四边形BCDE}}$的值.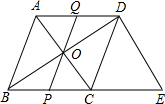 在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6,过D点作DE∥AC交BC的延长线于点E.
在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6,过D点作DE∥AC交BC的延长线于点E.