题目内容
3．计算：（a+2-$\frac{5}{a-2}$）•$\frac{2a-4}{3-a}$．分析 首先将括号里面通分运算，进而利用分式的性质化简求出即可．
解答 解：（a+2-$\frac{5}{a-2}$）•$\frac{2a-4}{3-a}$
=[$\frac{（a+2）（a-2）}{a-2}$-$\frac{5}{a-2}$]×$\frac{2（a-2）}{3-a}$
=$\frac{（a-3）（a+3）}{a-2}$×$\frac{2（a-2）}{3-a}$
=-2a-6．
点评 此题主要考查了分式的混合运算，正确进行通分运算是解题关键．
练习册系列答案
相关题目
13．若a＜b，则下列不等式中正确的是（ ）
| A． | a-3＜b-3 | B． | a-b＞0 | C． | $\frac{1}{3}a＞\frac{1}{3}$b | D． | -2a＜-2b |
14．
如图，正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A，B两点，其中点A的横坐标为2，当y1＞y2时，x的取值范围是（ ）
如图，正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A，B两点，其中点A的横坐标为2，当y1＞y2时，x的取值范围是（ ）| A． | x＜-2或x＞2 | B． | x＜-2或0＜x＜2 | C． | -2＜x＜0或0＜x＜2 | D． | -2＜x＜0或x＞2 |
18．计算3+（-3）的结果是（ ）
| A． | 6 | B． | -6 | C． | 1 | D． | 0 |
8．一个等腰三角形的两条边长分别是方程x2-7x+10=0的两根，则该等腰三角形的周长是（ ）
| A． | 12 | B． | 9 | C． | 13 | D． | 12或9 |
15．关于x的一元二次方程（m-2）x2+2x+1=0有实数根，则m的取值范围是（ ）
| A． | m≤3 | B． | m＜3 | C． | m＜3且m≠2 | D． | m≤3且m≠2 |
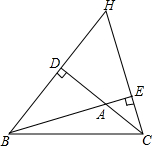已知BD、CE是△ABC的两条高，直线BD、CE相交于点H．