题目内容
 如图,平行四边形AECF中,B、D是直线EF上的点,且AD=BC,求证:四边形ABCD是平行四边形.
如图,平行四边形AECF中,B、D是直线EF上的点,且AD=BC,求证:四边形ABCD是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:过点A作AG⊥EF于G,作CH⊥EF于H,根据平行四边形的性质可得AG=CH,再利用“HL”证明Rt△ADG和Rt△CBH全等,根据全等三角形对应角相等可得∠ADG=∠CBH,然后根据内错角相等,两直线平行可得AD∥BC,再根据一组对边平行且相等的四边形是平行四边形证明即可.
解答: 证明:如图,过点A作AG⊥EF于G,作CH⊥EF于H,
证明:如图,过点A作AG⊥EF于G,作CH⊥EF于H,
∵四边形AECF是平行四边形,
∴AG=CH,
在Rt△ADG和Rt△CBH中,
,
∴Rt△ADG≌Rt△CBH(HL),
∴∠ADG=∠CBH,
∴AD∥BC,
又∵AD=BC,
∴四边形ABCD是平行四边形.
 证明:如图,过点A作AG⊥EF于G,作CH⊥EF于H,
证明:如图,过点A作AG⊥EF于G,作CH⊥EF于H,∵四边形AECF是平行四边形,
∴AG=CH,
在Rt△ADG和Rt△CBH中,
|
∴Rt△ADG≌Rt△CBH(HL),
∴∠ADG=∠CBH,
∴AD∥BC,
又∵AD=BC,
∴四边形ABCD是平行四边形.
点评:本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定方法和性质并作辅助线构造成全等三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知∠1=28°,∠2=96°,∠3=39°,则∠4的度数是( )
如图,已知∠1=28°,∠2=96°,∠3=39°,则∠4的度数是( )| A、17° | B、30° |
| C、45° | D、69° |
下列式子不正确的是( )
| A、|-3|=3 | ||||
B、|
| ||||
| C、|-2.5|=-2.5 | ||||
| D、|0|=0 |
将抛物线y=x2向上平移3个单位,再向下平移2个单位,那么得到的抛物线解析式为( )
| A、y=(x-2)2+3 |
| B、y=(x+2)2+3 |
| C、y=(x+2)2-3 |
| D、y=(x-2)2-3 |
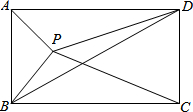 如图,在平行四边形ABCD中,P是△BAD内一点.若△PAB的面积为2,△PCB的面积为5,求△PBD的面积.
如图,在平行四边形ABCD中,P是△BAD内一点.若△PAB的面积为2,△PCB的面积为5,求△PBD的面积. 已知,如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CD于H.判断∠5、∠6的数量关系,并说明理由.
已知,如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CD于H.判断∠5、∠6的数量关系,并说明理由. 如图,正六边形ABCDEF的面积为54cm2,AP=2PF,CQ=2BQ.求四边形CEPQ的面积.
如图,正六边形ABCDEF的面积为54cm2,AP=2PF,CQ=2BQ.求四边形CEPQ的面积.