题目内容
7777的末尾数字的绝对值的平方为a,且a+b=0,则(a2+b)10•(a-b)5为多少?
考点:尾数特征
专题:
分析:先分别求出71、72、73、74、75、76的数值可得出末位数成规律变化,继而可得出7777的末位数字,进一步求出a、b,进一步代入求得数值即可.
解答:解:71=7,72=49、73=343、74=2401、75=16807、76=117649,
所以可得出个位数分别为7、9、3、1且呈周期性变化每4个7相乘一个周期,777÷4=194…1,则:
7777的末位数字是7,
∴a=72=49,a+b=0,b=-49,
∴(a2+b)10×(a-b)5
=(492-49)10×[49-(-49)]5
=4915×4810×25.
所以可得出个位数分别为7、9、3、1且呈周期性变化每4个7相乘一个周期,777÷4=194…1,则:
7777的末位数字是7,
∴a=72=49,a+b=0,b=-49,
∴(a2+b)10×(a-b)5
=(492-49)10×[49-(-49)]5
=4915×4810×25.
点评:此题考查乘方末尾数字的特点,找出规律,解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程x2=x的根是( )
| A、x=1 |
| B、x=-1 |
| C、x=0 |
| D、x1=0,x2=1 |
下列数据能作为三角形三边长的一组是( )
| A、1cm、2cm、3cm |
| B、1cm、2cm、4cm |
| C、2cm、3cm、4cm |
| D、4cm、4cm、9cm |
 如图,平行四边形AECF中,B、D是直线EF上的点,且AD=BC,求证:四边形ABCD是平行四边形.
如图,平行四边形AECF中,B、D是直线EF上的点,且AD=BC,求证:四边形ABCD是平行四边形.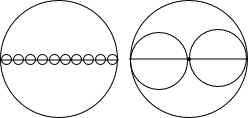 如图,两个大小相同的大圆,其中一个大圆内有10个小圆,另一个大圆内有2个小圆,你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大?请你猜一猜,并用学过的知识和数学方法验证你的猜想.
如图,两个大小相同的大圆,其中一个大圆内有10个小圆,另一个大圆内有2个小圆,你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大?请你猜一猜,并用学过的知识和数学方法验证你的猜想. 如图,AB,AC为⊙O的两条弦,且AB=AC,D为
如图,AB,AC为⊙O的两条弦,且AB=AC,D为