题目内容
3．如图正六边形ABCDEF．请分别在图1，图2中使用无刻度的直尺按要求画图．（1）在图1中，画出一个与正六边形的边长相等的菱形；
（2）在图2中，画一个边长与正六边形的边长不相等的菱形．
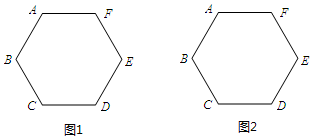
分析 （1）连接AD、BE交于点O，四边形AOEF即为所求；
（2）连接AC、DF、BF、CE，菱形FGCH即为所求；或延长AB、DC交于点G，延长AF、DE交于点H，菱形AGDH即为所求．
解答 解：（1）画图如下：四边形AOEF（或四边形BCDO）即为所求；
（2）画图如下：解法一：菱形FGCH即为所求．
解法二：菱形AGDH即为所求．
点评 本题主要考查作图-复杂作图，熟练掌握正六边形的性质和菱形的判定是解题的关键．
练习册系列答案
相关题目
，则下列各式中一定成立的是（ ）
B. 
C. 
D. 
14．
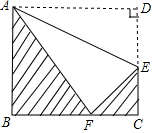如图，将长方形纸片ABCD沿直线AE折叠，顶点D恰好落在BC边上点F处，已知CE=3cm，AB=8cm，图中阴影部分的面积是（ ）
如图，将长方形纸片ABCD沿直线AE折叠，顶点D恰好落在BC边上点F处，已知CE=3cm，AB=8cm，图中阴影部分的面积是（ ）| A． | 80cm2 | B． | 50cm2 | C． | 30cm2 | D． | 20cm2 |
8．如果（a-1）x2+ax+a2-1=0是关于x的一元二次方程，那么必有（ ）
| A． | a≠0 | B． | a≠1 | C． | a≠-1 | D． | a=±-1 |
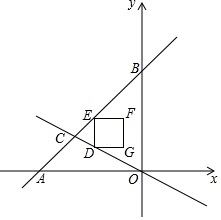如图，直线y=x+6与x轴交于点A，与y轴交于点B，与直线y=-$\frac{1}{2}$x交于点C，D为线段OC上的动点，D与C，O不重合，作DE∥OB交AB于E，以DE为边在DE的右侧作正方形DEFO，正方形DEFG与△BOC重叠部分的面积为S，D点的横坐标为x，求S与x的函数关系式．
12．
如图所示，已知CD平分∠ACB，DE∥AC，∠1=30°，则∠2=（ ）
如图所示，已知CD平分∠ACB，DE∥AC，∠1=30°，则∠2=（ ）| A． | 35° | B． | 30° | C． | 50° | D． | 60° |
13．由$\frac{x}{3}$-y=6，可以得到用x表示y的式子是（ ）
| A． | x=18-y | B． | x=18-3y | C． | y=$\frac{x}{3}$-6 | D． | y=$\frac{x}{3}$+6 |