题目内容
18.已知:?ABCD的两边AB、AD的长是关于x的方程x2-mx+$\frac{\sqrt{3}}{2}$m-$\frac{3}{4}$=0的两个实数根.(1)m为何值时,四边形ABCD是菱形?
(2)若AB的长为2$\sqrt{3}$,则?ABCD的周长是多少?
分析 (1)根据菱形的判定方法,当AB=AD时,?ABCD为菱形,再利用根的判别式的意义得到△=m2-4($\frac{\sqrt{3}}{2}$m-$\frac{3}{4}$)=0,然后解关于m的方程即可;
(2)利用方程根的定义,把x=2$\sqrt{3}$代入方程x2-mx+$\frac{\sqrt{3}}{2}$m-$\frac{3}{4}$=0可求出m=$\frac{5\sqrt{3}}{2}$,则方程化为x2-$\frac{5\sqrt{3}}{2}$x+3=0,再解方程AD=$\frac{\sqrt{3}}{2}$,然后计算?ABCD的周长.
解答 解:(1)当AB=AD时,?ABCD为菱形,
此时方程x2-mx+$\frac{\sqrt{3}}{2}$m-$\frac{3}{4}$=0的两个相等的实数根,
所以△=m2-4($\frac{\sqrt{3}}{2}$m-$\frac{3}{4}$)=0,解得m1=m2=$\sqrt{3}$,
即m为$\sqrt{3}$时,四边形ABCD是菱形;
(2)根据题意得2$\sqrt{3}$为关于x的方程x2-mx+$\frac{\sqrt{3}}{2}$m-$\frac{3}{4}$=0的实数根,
所以12-2$\sqrt{3}$m+$\frac{\sqrt{3}}{2}$m-$\frac{3}{4}$=0,解得m=$\frac{5\sqrt{3}}{2}$
方程化为x2-$\frac{5\sqrt{3}}{2}$x+3=0,解得x1=$\frac{\sqrt{3}}{2}$,x2=2$\sqrt{3}$,
即AB=2$\sqrt{3}$,AD=$\frac{\sqrt{3}}{2}$,
所以?ABCD的周长=2(AB+AD)=4$\sqrt{3}$+$\sqrt{3}$=5$\sqrt{3}$.
点评 本题考查了菱形的判定与性质:菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.也考查了根的判别式.

| A. | $\sqrt{({-9)}^{2}}$=-9 | B. | $\sqrt{25}$=±5 | C. | $\root{3}{-27}$=-3 | D. | (-$\sqrt{2}$)2=-2 |
 某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为( )人.
某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为( )人.| A. | 120 | B. | 110 | C. | 100 | D. | 80 |
| A. | 5,12,13 | B. | 12,13,14 | C. | 3,4,5 | D. | 7,24,25 |
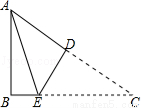
 如图,若∠ADE=∠ABC,则DE∥BC,理由:同位角相等,两直线平行.
如图,若∠ADE=∠ABC,则DE∥BC,理由:同位角相等,两直线平行.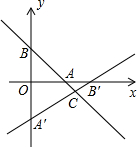 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴,y轴于点A,B,直线A′B′分别交x轴,y轴于点B′,A′,且△AOB≌△A′OB′.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴,y轴于点A,B,直线A′B′分别交x轴,y轴于点B′,A′,且△AOB≌△A′OB′.