题目内容
6.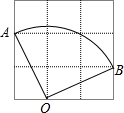 如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$.
如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是$\frac{5π}{4}$.
分析 根据题意知,该扇形的圆心角是90°.根据勾股定理可以求得OA=OB=$\sqrt{5}$,由扇形面积公式可得出结论.
解答 解:∵每个小方格都是边长为1的正方形,
∴OA=OB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴S扇形OAB=$\frac{90π×(\sqrt{5})^{2}}{360}$=$\frac{90π×5}{360}$=$\frac{5π}{4}$.
故答案为:$\frac{5π}{4}$.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
14.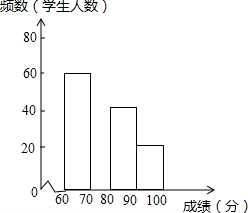 在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题:
(1)在频数分布表中,m=80,n=0.2.
(2)请补全图中的频数分布直方图.
(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参赛,请估计约有多少人进入决赛?
 在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:根据所给信息,解答下列问题:
(1)在频数分布表中,m=80,n=0.2.
| 成绩 | 频数 | 频率 |
| 60≤x<70 | 60 | 0.30 |
| 70≤x<80 | m | 0.40 |
| 80≤x<90 | 40 | n |
| 90≤x≤100 | 20 | 0.10 |
(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参赛,请估计约有多少人进入决赛?
11.已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
| A. | a=5,b=1 | B. | a=-5,b=1 | C. | a=5,b=-1 | D. | a=-5,b=-1 |
15.东营市某学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化试题10道,实践应用试题6道,创新能力试题4道.小婕从中任选一道试题作答,他选中创新能力试题的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
16.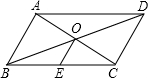 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )| A. | OE=$\frac{1}{2}$DC | B. | OA=OC | C. | ∠BOE=∠OBA | D. | ∠OBE=∠OCE |
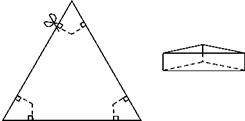 如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.
如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.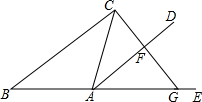 如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.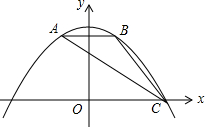 如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,$\frac{9}{4}$),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,$\frac{9}{4}$),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上. 已知反比例函数y=$\frac{4}{x}$.
已知反比例函数y=$\frac{4}{x}$.