题目内容
4．一元二次方程x2-6x-5=0配方后可变形为（ ）| A． | （x-3）2=14 | B． | （x-3）2=4 | C． | （x+3）2=14 | D． | （x+3）2=4 |
分析 先把方程的常数项移到右边，然后方程两边都加上32，这样方程左边就为完全平方式．
解答 解：x2-6x-5=0，
x2-6x=5，
x2-6x+9=5+9，
（x-3）2=14，
故选：A．
点评 本题考查了利用配方法解一元二次方程ax2+bx+c=0（a≠0）：先把二次系数变为1，即方程两边除以a，然后把常数项移到方程右边，再把方程两边加上一次项系数的一半．
练习册系列答案
相关题目
14．
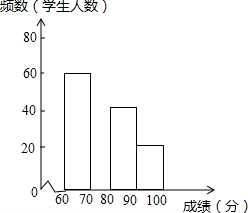在2016CCTV英语风采大赛中，娄底市参赛选手表现突出，成绩均不低于60分．为了更好地了解娄底赛区的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行了整理，得到如图的两幅不完整的统计图表：
根据所给信息，解答下列问题：
（1）在频数分布表中，m=80，n=0.2．
（2）请补全图中的频数分布直方图．
（3）按规定，成绩在80分以上（包括80分）的选手进入决赛．若娄底市共有4000人参赛，请估计约有多少人进入决赛？
在2016CCTV英语风采大赛中，娄底市参赛选手表现突出，成绩均不低于60分．为了更好地了解娄底赛区的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行了整理，得到如图的两幅不完整的统计图表：根据所给信息，解答下列问题：
（1）在频数分布表中，m=80，n=0.2．
| 成绩 | 频数 | 频率 |
| 60≤x＜70 | 60 | 0.30 |
| 70≤x＜80 | m | 0.40 |
| 80≤x＜90 | 40 | n |
| 90≤x≤100 | 20 | 0.10 |
（3）按规定，成绩在80分以上（包括80分）的选手进入决赛．若娄底市共有4000人参赛，请估计约有多少人进入决赛？
15．东营市某学校组织知识竞赛，共设有20道试题，其中有关中国优秀传统文化试题10道，实践应用试题6道，创新能力试题4道．小婕从中任选一道试题作答，他选中创新能力试题的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{3}{10}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{2}$ |
19．不等式组$\left\{\begin{array}{l}{x+1≥2}\\{\frac{x}{2}≤1}\end{array}\right.$的解集是（ ）
| A． | x≤1 | B． | x≥2 | C． | 1≤x≤2 | D． | 1＜x＜2 |
16．
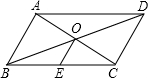已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（ ）
已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（ ）| A． | OE=$\frac{1}{2}$DC | B． | OA=OC | C． | ∠BOE=∠OBA | D． | ∠OBE=∠OCE |
13．
今年5月，某大型商业集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．
根据以上信息解答下列问题：
（1）求m的值；
（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；（结果用度、分、秒表示）
（3）从评估成绩不少于80分的连锁店中任选2家介绍营销经验，求其中至少有一家是A等级的概率．
今年5月，某大型商业集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．| 评估成绩n（分） | 评定等级 | 频数 |
| 90≤n≤100 | A | 2 |
| 80≤n＜90 | B | |
| 70≤n＜80 | C | 15 |
| n＜70 | D | 6 |
（1）求m的值；
（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；（结果用度、分、秒表示）
（3）从评估成绩不少于80分的连锁店中任选2家介绍营销经验，求其中至少有一家是A等级的概率．
19．非零数a的倒数是（ ）
| A． | a | B． | |a| | C． | $\frac{1}{a}$ | D． | -a |