题目内容
5.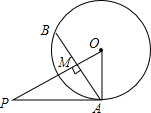 如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为( )
如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
分析 先根据垂径定理得AM=$\frac{1}{2}$AB=2,则利用勾股定理可计算出OA=$\sqrt{5}$,再根据切线的性质得∠OAP=90°,即∠PAM+∠OAM=90°,利用等角的余角相等得∠P=∠OAM,于是可判断Rt△PAM∽Rt△AOM,然后利用相似比可计算出PA的长.
解答 解:∵AB⊥OP,
∴AM=BM=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2,
在Rt△AOM中,OA=$\sqrt{O{A}^{2}+A{M}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵PA切⊙O于点A,
∴OA⊥PA,
∴∠OAP=90°,即∠PAM+∠OAM=90°,
而∠PAM+∠P=90°,
∴∠P=∠OAM,
∴Rt△PAM∽Rt△AOM,
∴$\frac{PA}{OA}$=$\frac{AM}{OM}$,即$\frac{PA}{\sqrt{5}}$=$\frac{2}{1}$,
∴PA=2$\sqrt{5}$.
故选C.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
17.下列事件发生的概率为0的是( )
| A. | 射击运动员只射击1次,就命中靶心 | |
| B. | 任取一个实数x,都有|x|≥0 | |
| C. | 画一个三角形,使其三边的长分别为8cm,6cm,2cm | |
| D. | 抛掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6 |
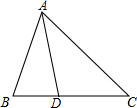 如图,已知△ABC,D是BC上的点,连接AD
如图,已知△ABC,D是BC上的点,连接AD



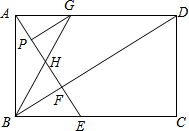 如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论:
如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论: