题目内容

7．设x1，x2是方程x2-x-2012=0的两实数根，则x13+2013x2-2010=2015．

分析 先根据一元二次方程的解的定义得到x12=x1+2012，再计算x13=x12+2012x1=2013x1+2012，则原式可化简为2013（x1+x2）+2，然后利用根与系数的关系求解．

解答 解：∵x1是方程x2-x-2012=0的实数根，
∴x12=x1+2012，
∴x13=x12+2012x1=x1+2012+2012x1=2013x1+2012，
∴原式=2013x1+2012+2013x2-2010=2013（x1+x2）+2，
∵x1，x2是方程x2-x-2012=0的两实数根，
∴x1+x2=1，
∴原式=2013+2=2015．
故答案为：2015．

点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．

练习册系列答案
相关题目
17．在-（-9），（-1）2013，-33，-|-2|中，负数共有（　　）
A．1个B．2个C．3个D．4个
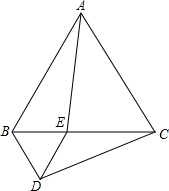18．如图，等边三角形ABC的边长为4，点E是边BC上一动点（不与点B、C重合），以BE为边在BC的下方作等边三角形BDE，连接AE、CD．
（1）在运动的过程中，AE与CD有何数量关系？请说明理由．
（2）当BE=2时，求∠BDC的度数．
15．在-4，0，π，1.010010001…，$\frac{22}{7}$，1.$\stackrel{•}{3}$这些数中，无理数有2个．
2．（1）当a=2，b=1时时，分别求代数式①a2-2ab+b2 ②（a-b）2 的值．
（2）当a=5，b=-3时，分别求代数式①a2-2ab+b2 ②（a-b）2的值．
（3）观察（1）（2）中代数式的值，a2-2ab+b2 与（a-b）2有何关系？
（4）利用你发现的规律，求135.72-2×135.7×35.7+35.72的值．
12．以下列各组长度的线段为边，能构成三角形的是（　　）
A．3，4，5B．7，3，4C．5，6，12D．1，2，3
19．先化简．再求值：$\frac{1}{2}$x-3（x-$\frac{1}{3}$y2）-（-$\frac{3}{2}$x+$\frac{1}{3}$y2），其中x=-2，y=-$\frac{3}{2}$．
16．观察如图图形：

它们是按一定规律排列的，依照此规律，第2015个图形共有6046个★．
17．某课外兴趣小组为了了解所在地区老年人的健康状况，分别做了下列四种不同的抽样调查：
①在公园调查了1 000名老年人的健康状况；
②在医院调查了1 000名老年人的健康状况；
③调查了10名老年邻居的健康状况；
④利用派出所的户籍网随机调查了该地区10%的老年人的健康状况．
你认为抽样比较合理的是④（填序号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网