题目内容
11.已知不等式$\frac{1}{3}$(x-6)<x-$\frac{2}{3}$,回答下列问题:(1)判断-2,1,0,-3是不是不等式的解?
(2)如果x=a-1是不等式的解,那么a的取值范围是多少?
分析 (1)求出不等式$\frac{1}{3}$(x-6)<x-$\frac{2}{3}$的解集,根据不等式的解得概念判断可得;
(2)由解的概念可知a-1>-2,解不等式可得.
解答 解:(1)解不等式$\frac{1}{3}$(x-6)<x-$\frac{2}{3}$,得:x>-2,
∴1、0是不等式的解集;
(2)∵x=a-1是不等式的解,
∴a-1>-2,
解得:a>-1.
点评 本题考查了不等式的解的定义:使不等式成立的未知数的值叫做不等式的解.正确求出不等式的解集是解题的关键.解不等式要依据不等式的基本性质.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
3.下列式子:①-7<0;②3x+1>0;③x≥2;④x-6.其中,是不等式的有( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
1.如果a>b,那么下列不等式中一定成立的是( )
| A. | a2>b2 | B. | 1-a>1-b | C. | 1+a>1-b | D. | 1+a>b-1 |
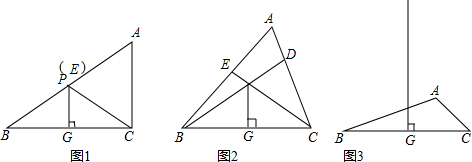
 如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.
如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.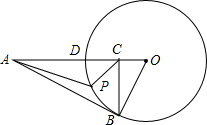 如图,AB切⊙O于B,BC⊥AO于C,AO交⊙O于D,BO=2,AO=8,P是弧BD上任一点,设k=$\frac{PA}{PC}$,问k的值是否随点P的移动而变化?证明你的结论.
如图,AB切⊙O于B,BC⊥AO于C,AO交⊙O于D,BO=2,AO=8,P是弧BD上任一点,设k=$\frac{PA}{PC}$,问k的值是否随点P的移动而变化?证明你的结论.