题目内容
7.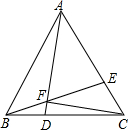 如图,边长为1的等边三角形ABC,D、E分别是BC、CA上的点,且有BD=CE,AD与BE交于点F,若AD⊥CF,则BD长为$\frac{1}{3}$.
如图,边长为1的等边三角形ABC,D、E分别是BC、CA上的点,且有BD=CE,AD与BE交于点F,若AD⊥CF,则BD长为$\frac{1}{3}$.
分析 根据题意推知△ADB≌△BEC(SAS),结合全等三角形的性质和相似三角形的判定得到:△AEF∽△ADC,由此得出比例式,再由勾股定理列出方程,联立方程组求出BD的长度.
解答  解:∵三角形ABC是等边三角形,
解:∵三角形ABC是等边三角形,
∴AB=BC,∠C=∠ABD=60°,
在△ADB和△BEC中$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$,
∴△ADB≌△BEC(SAS),
∴∠BAD=∠CBE,
又∵BD=CE,
∴∠BAD+∠ABF=60°,即∠AFE=60°.
在△AEF和△ADC中,∠AFE=∠ACB,∠DAC=∠EAF,
∴△AEF∽△ADC,
∴$\frac{AF}{AC}$=$\frac{AE}{AD}$.
设BD=x,DF=m,DA=n,
则x2=mn①
$\frac{n-m}{1}$=$\frac{1-x}{n}$,
∴n2-mn=1-x②
又∵AD⊥CF,
∴AC2-AF2=CD2-DF2,
∴12-(n-m)2=(1-x)2-m2③.
由①②③可得:x=$\frac{1}{3}$,即BD=$\frac{1}{3}$.
故答案是:$\frac{1}{3}$.
点评 本题考查了等边三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识点的应用,题目比较好,难度偏大.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
2.已知Rt△ABC中,a、b为直角边,c为斜边,h为斜边上的高,则下面说法错误的是( )
| A. | ab=ch | |
| B. | h<a | |
| C. | 以ah、bh、ab为边的三角形是直角三角形 | |
| D. | 以a+b、ab、c为边的三角形是直角三角形 |
 如图,在平面直角坐标系中,点P的坐标为(0,8),直线y=$\frac{3}{4}$x-6与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{56}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,8),直线y=$\frac{3}{4}$x-6与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{56}{5}$.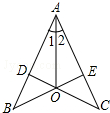 如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O,图中有3对全等的直角三角形.
如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O,图中有3对全等的直角三角形. 如图:在△ABC中,DE∥FG∥BC,且DE、FG将△ABC的面积三等分,若AB=BC=12cm,求FG和DF的长.
如图:在△ABC中,DE∥FG∥BC,且DE、FG将△ABC的面积三等分,若AB=BC=12cm,求FG和DF的长.