题目内容
解方程：
（1）x2-4x+1=0；
（2）x2-x-2=0；
（3）（y2+2y）-7y+14=0．
（1）x2-4x+1=0；
（2）x2-x-2=0；
（3）（y2+2y）-7y+14=0．
考点：解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题：计算题
分析：（1）利用配方法解方程；
（2）利用因式分解法解方程；
（3）先计算判别式的值，然后根据判别式的意义判断根的情况．
（2）利用因式分解法解方程；
（3）先计算判别式的值，然后根据判别式的意义判断根的情况．
解答：解：（1）x2-4x+4=3，
（x-2）2=3，
x-2=±
，
所以x1=2+
，x2=2-
；
（2）（x-2）（x+1）=0，
x-2=0或x+1=0，
所以x1=2，x2=-1；
（3）y2-5y+14=0．
△=52-4×1×14＜0，
所以方程没有实数解．
（x-2）2=3，
x-2=±
| 3 |
所以x1=2+
| 3 |
| 3 |
（2）（x-2）（x+1）=0，
x-2=0或x+1=0，
所以x1=2，x2=-1；
（3）y2-5y+14=0．
△=52-4×1×14＜0，
所以方程没有实数解．
点评：本题考查了解一元二次方程-因式分解法：先把方程右边变形为0，然后把方程左边进行因式分解，这样把一元二次方程转化为两个一元一次方程，再解一次方程可得到一元二次方程的解．也考查了配方法解一元二次方程和根的判别式．
练习册系列答案
相关题目
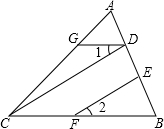已知：如图，∠AGD=∠ACB，∠1=∠2，CD与EF平行吗？为什么？