题目内容
20.已知一次函数y=2x+b.(1)它的图象与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图象经过一次函数y=-2x+1,y=x+4图象的交点,求b的值.
分析 (1)可先求出直线y=2x+b与两坐标轴的交点坐标,然后根据条件就可解决问题;
(2)可先求出直线y=-2x+1与y=x+4图象的交点,然后把交点坐标代入y=2x+b,就可解决问题.
解答 解:(1)令x=0,得y=b;令y=0,得x=-$\frac{b}{2}$,
∴S=$\frac{1}{2}$|b|•|-$\frac{b}{2}$|=$\frac{1}{4}$•|b2|=4,
∴b=±4;
(2)解$\left\{\begin{array}{l}{y=-2x+1}\\{y=x+4}\end{array}\right.$,
得$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$,
把x=-1,y=3代入y=2x+b,
得b=5.
点评 本题主要考查了直线上点的坐标特征、求两直线的交点坐标等知识,需要注意的是,将点的坐标转化为线段长度时,要用坐标的绝对值表示线段的长度.

练习册系列答案
相关题目
10.单项式-3xy2z2的系数和次数分别是( )
| A. | -3,4 | B. | -3,5 | C. | 3,6 | D. | 3,5 |
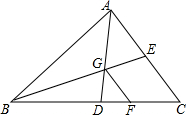 如图,已知点G为△ABC的重心,GF∥AC,求DF:FC、BC:BF的值.
如图,已知点G为△ABC的重心,GF∥AC,求DF:FC、BC:BF的值. 已知AB∥DE,BF、DF分别平分∠ABC,∠CDE,求∠C、∠F的关系.
已知AB∥DE,BF、DF分别平分∠ABC,∠CDE,求∠C、∠F的关系.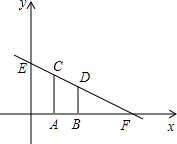 在平面直角坐标系中,CA⊥x轴于点A(1,0),BD⊥x轴于点B(3,0),直线CD与x轴,y轴分别交于点F,E,且解析式y=kx+3,S四边形ABCD=4,求直线CD的解析式.
在平面直角坐标系中,CA⊥x轴于点A(1,0),BD⊥x轴于点B(3,0),直线CD与x轴,y轴分别交于点F,E,且解析式y=kx+3,S四边形ABCD=4,求直线CD的解析式.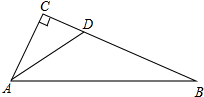 如图所示,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=$\sqrt{3}$,sinB=$\frac{1}{2}$,BD=2$\sqrt{3}$,求AC,AB的长.
如图所示,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=$\sqrt{3}$,sinB=$\frac{1}{2}$,BD=2$\sqrt{3}$,求AC,AB的长. 如图:
如图: