题目内容
9.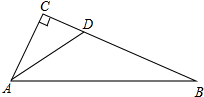 如图所示,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=$\sqrt{3}$,sinB=$\frac{1}{2}$,BD=2$\sqrt{3}$,求AC,AB的长.
如图所示,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=$\sqrt{3}$,sinB=$\frac{1}{2}$,BD=2$\sqrt{3}$,求AC,AB的长.
分析 设AC=x,根据正弦的概念用x表示出AB的长,根据勾股定理列出方程,解方程即可.
解答 解:∵CD=$\sqrt{3}$,BD=2$\sqrt{3}$,
∴BC=3$\sqrt{3}$,
设AC=x,
∵sinB=$\frac{1}{2}$,
∴$\frac{AC}{AB}$=$\frac{1}{2}$,
∴AB=2x,
由勾股定理得,(2x)2=x2+(3$\sqrt{3}$)2,
解得x=3,
则2x=6,
∴AC=3,AB=6.
点评 本题考查的是勾股定理的应用、角平分线的定义和解直角三角形的应用,掌握直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解题的关键,解答时注意正弦的概念的应用.

练习册系列答案
相关题目