题目内容
5.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边.a+b=2,∠B=60°,则c=2$\sqrt{3}$-2.分析 根据三角形的内角和公式可求得∠A的度数,根据三角函数和已知可求得a的值然后根据含30°角的直角三角形的性质即可得到结论.
解答 解:∵∠C=90°,∠B=60°,
∴∠A=90°-∠B=30°,
∵tanB=$\frac{b}{a}$,∴b=$\sqrt{3}$a,
∵a+b=2,
∴a=$\sqrt{3}$-1,
∵∴c=2a=2$\sqrt{3}$-2.
故答案为:2$\sqrt{3}$-2.
点评 本题考查了含30°角的直角三角形的性质,三角形的内角和,三角函数,熟记含30°角的直角三角形的性质是解题的关键.

练习册系列答案
相关题目
10.抛物线的对称轴为直线x=3,y的最大值为-5,且与y=$\frac{1}{2}$x2的图象开口大小相同.则这条抛物线解析式为( )
| A. | y=-$\frac{1}{2}$(x+3)2+5 | B. | y=-$\frac{1}{2}$(x-3)2-5 | C. | y=$\frac{1}{2}$(x+3)2+5 | D. | y=$\frac{1}{2}$(x-3)2-5 |
15.下列说法中,正确的是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 经过一点,有且只有一条直线与已知直线平行 | |
| C. | 过线段外任一点,可以作它的垂直平分线 | |
| D. | 在同一平面内,垂直于同一条直线的两条直线互相平行 |
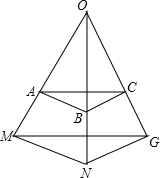 如图,已知AB∥MN,BC∥NG.求证:$\frac{OA}{OM}$=$\frac{OC}{OG}$.
如图,已知AB∥MN,BC∥NG.求证:$\frac{OA}{OM}$=$\frac{OC}{OG}$.