题目内容
18. 如图,AC,BD相交于点O,且OA=OB,OC=OD,则图中全等的三角形有3对.
如图,AC,BD相交于点O,且OA=OB,OC=OD,则图中全等的三角形有3对.
分析 由OA=OB,OC=OD,∠AOD=∠BOC,根据“SAS”可判断△AOD≌△BOC,则AD=BC,然后根据“SSS”可判断△ABD≌△BAC,△ADC≌△BCD.
解答 解:在△AOD与△BOC中,
$\left\{\begin{array}{l}{OA=OB}\\{∠AOD=∠BOC}\\{OD=OC}\end{array}\right.$,
∴△AOD≌△BOC(SAS);
∴AD=BC,
而OA+OC=OD+OB,即AC=DB,
在△ABD与△BAC中,
$\left\{\begin{array}{l}{AD=BC}\\{BD=AC}\\{AB=AB}\end{array}\right.$,
∴△ABD≌△BAC(SSS),
在△ADC与△BCD中,
$\left\{\begin{array}{l}{AD=BC}\\{AC=BD}\\{DC=DC}\end{array}\right.$,
∴△ADC≌△BCD(SSS).
故答案为3.
点评 本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”.

练习册系列答案
相关题目
9. 如图,在△ABC中,∠A=110°,DE∥CB,若∠CDE=140°,则∠B的度数为( )
如图,在△ABC中,∠A=110°,DE∥CB,若∠CDE=140°,则∠B的度数为( )
 如图,在△ABC中,∠A=110°,DE∥CB,若∠CDE=140°,则∠B的度数为( )
如图,在△ABC中,∠A=110°,DE∥CB,若∠CDE=140°,则∠B的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
6.若x满足x2=$\frac{9}{4}$,则x的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | ±$\frac{3}{2}$ | D. | ±$\frac{2}{3}$ |
 如图所示.已知$\frac{AB}{BD}=\frac{BC}{BE}=\frac{CA}{ED}$,判断∠BAD和∠BCE是否相等?说明理由.
如图所示.已知$\frac{AB}{BD}=\frac{BC}{BE}=\frac{CA}{ED}$,判断∠BAD和∠BCE是否相等?说明理由.
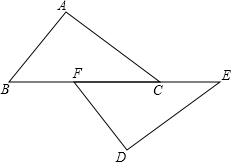 如图,点B、F、C、E在一条直线上,AB=DE,FB=CE,AC=DF,求证:△ABC≌△DEF.
如图,点B、F、C、E在一条直线上,AB=DE,FB=CE,AC=DF,求证:△ABC≌△DEF.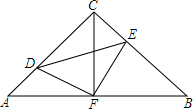 如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16.
如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16.