题目内容
16．已知x1，x2是方程2x2+4x-1=0的两个实数根，求$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$的值．分析 由韦达定理可得x1+x2=-2，x1x2=-$\frac{1}{2}$，代入到$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{（x}_{1}+{x}_{2}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$即可得答案．
解答 解：∵x1，x2是方程2x2+4x-1=0的两个实数根，
∴x1+x2=-2，x1x2=-$\frac{1}{2}$，
则$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{（x}_{1}+{x}_{2}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{4+1}{-\frac{1}{2}}$=-10．
点评 本题主要考查根与系数的关系，熟练掌握韦达定理是解题的关键．
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
如图，MN是⊙O的直径．
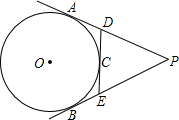如图，PA、PB分别切⊙O于A、B两点，过劣弧$\widehat{AB}$上的一点C作⊙O的切线分别交PA、PB于D、E．求证：∠DOE=90°-$\frac{1}{2}$∠P．
上海世博会区间，某博物馆每周都吸引大量中外游客前来参观，如果游客过多，对馆中的珍贵文物会产生不利影响，但同时考虑到文物的修缮和保存费用问题，还要保证一定的门票收入．因此，博物馆采取了涨浮门票价格的方法来控制参观人数，在该方法实施过程中发现：每周参观人数与票价之间存在着如图所示的一次函数关系，在这样的情况下．
如图所示，点P是射线OC上任意一点，PD⊥OA于点D，PE⊥OB于点E，当OC平分∠AOB时，可以得到PD=PE，反过来，当PD=PE时，OC平分∠AOB吗？为什么？