题目内容
9. 如图所示,点P是射线OC上任意一点,PD⊥OA于点D,PE⊥OB于点E,当OC平分∠AOB时,可以得到PD=PE,反过来,当PD=PE时,OC平分∠AOB吗?为什么?
如图所示,点P是射线OC上任意一点,PD⊥OA于点D,PE⊥OB于点E,当OC平分∠AOB时,可以得到PD=PE,反过来,当PD=PE时,OC平分∠AOB吗?为什么?
分析 根据题意得出△OPD≌△OPE,进而可得出结论.
解答 解:OC平分∠AOB.
理由:∵PD⊥OA于点D,PE⊥OB于点E,
∴∠PDO=∠PEO.
在Rt△OPD与Rt△OPE中,
∵$\left\{\begin{array}{l}{OP=OP}\\{PD=PE}\end{array}\right.$,
∴△OPD≌△OPE(HL),
∴∠DOP=∠EOP,即OC平分∠AOB.
点评 本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
18.已知x=-1是一元二次方程x2+mx+n=0的一个根,则(m-n)2的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
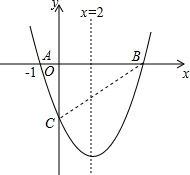 如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0),其顶点为D.
如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0),其顶点为D.