题目内容
19. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;
②a-b+c>0;
③4a+2b+c>0;
④b<-2a;
⑤a+b+c>am2+bm+c(m≠1的实数)
其中正确的结论有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①由图象可知:a<0,b>0,c>0,abc<0,故①正确;
②当x=-1时,y=a-b+c<0,即b>a+c,故②错误;
③当x=2时,y=4a+2b+c>0,故③正确;
④对称轴为x=-$\frac{b}{2a}$=1,b=-2a,故④错误;
⑤当x=1时,y的值最大.此时,y=a+b+c,
而当x=m时,y=am2+bm+c,
所以a+b+c>am2+bm+c,故⑤正确.
故①③⑤正确.
故选B.
点评 本题考查了考查了图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴和抛物线与y轴的交点、抛物线与x轴交点的个数确定.

练习册系列答案
相关题目
14. 如图,BC=24,E、F分别是线段AB和线段AC的中点,那么线段EF的长是( )
如图,BC=24,E、F分别是线段AB和线段AC的中点,那么线段EF的长是( )
 如图,BC=24,E、F分别是线段AB和线段AC的中点,那么线段EF的长是( )
如图,BC=24,E、F分别是线段AB和线段AC的中点,那么线段EF的长是( )| A. | 12 | B. | 10 | C. | 9 | D. | 16 |
4.下列各运算中,正确的是( )
| A. | a2+a3=a5 | B. | (a+1)2=a2+1 | C. | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$ | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
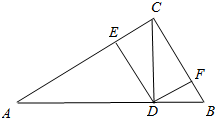 如图,CD是Rt△ABC斜边AB上的高,DE⊥AC,DF⊥BC,垂足分别为E,F.已知AC=8,BC=6.
如图,CD是Rt△ABC斜边AB上的高,DE⊥AC,DF⊥BC,垂足分别为E,F.已知AC=8,BC=6.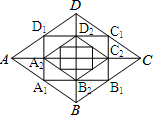 如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2011B2011C2011D2011的面积用含a,b的代数式表示为$\frac{ab}{{2}^{2012}}$.
如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2011B2011C2011D2011的面积用含a,b的代数式表示为$\frac{ab}{{2}^{2012}}$.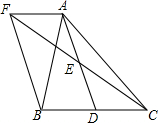 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.