题目内容
10.某校举行书法比赛活动,购买A,B两种毛笔作为奖品,A,B两种毛笔的单价分别为15元和10元,根据比赛设奖情况.需要购买两种毛笔共40支,且学校决定购买毛笔的资金不能超过500元.(1)求最多能购买A种毛笔多少支.
(2)若购买B种毛笔的数量要小于A种毛笔数量的2倍,则购买这两种毛笔各多少支时,费用最少?最少费用是多少?
分析 (1)设买A种毛笔x元,根据题意可得到一个一元一次不等式,解不等式可得到最多能购买A种毛笔的数量;
(2)根据“购买B种毛笔的数量要小于A种毛笔数量的2倍”可得出x的范围,再根据一次函数的增减性,即可求得最少花费.
解答 解:(1)设能买A种毛笔x本,则能买B种毛笔(40-x)本,
根据题意,得 15x+10(40-x)≤500,
解得:x≤20.
答:最多能购买A种毛笔20支;
(2)设购买A,B两种毛笔共花费W元,则:W=15x+10(40-x)=5x+400,
由题意,得:40-x<2x,
解得:x>$\frac{40}{3}$,
∵k=5>0.w随x的增大而增大,当x取最小时,花费最少,
又∵x>$\frac{40}{3}$,x为整数,
∴当x=14时,W最小=5×14+400=470(元).
答:购买A种笔记本14本,B种笔记本26本时,花费最少,此时的花费是470元.
点评 此题考查了一次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,将实际问题转化为一次函数的知识进行求解,难度一般.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
20.如图,用火柴棒搭图形,第1个图形用了三根火柴棒搭出了一个等边三角形,第二个图形在第一个图形的基础上搭了一个每边是一根火柴棒的平行四边形,平行四边形与三角形的公共边只用一根火柴棒,依次交替搭下去搭出以后各个图形,记第n个图形用了an根火柴棒.

(1)填表:
(2)当n为奇数时,小明说:an=5n+3,小亮说:an=$\frac{5n+1}{2}$.你认为他们谁说得对?
并求当n为偶数时的an(用含n的代数式表示).
(3)an是否可取下列各值:2016,2015?若可取,求出此时n的值.

(1)填表:
| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
并求当n为偶数时的an(用含n的代数式表示).
(3)an是否可取下列各值:2016,2015?若可取,求出此时n的值.
18.函数y=2x2+1有( )
| A. | 最大值1 | B. | 最小值1 | C. | 最大值0 | D. | 最小值0 |
5.若k为任意实数,则抛物线y=-2(x-k)2+k的顶点在( )
| A. | 直线y=x上 | B. | 直线y=-x上 | C. | x轴上 | D. | y轴上 |
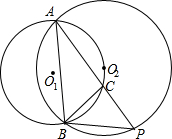 如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)
如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号) 如图,在△ABC中,D是BC上一点,且AB=BD=3CD,若cos∠DAC=$\frac{7}{8}$,AD=6,则AC=8.
如图,在△ABC中,D是BC上一点,且AB=BD=3CD,若cos∠DAC=$\frac{7}{8}$,AD=6,则AC=8.