题目内容
19.已知:关于x的方程x2+kx-2=0,(1)求证:无论k为何值,方程总有两个不相等的实数根.
(2)设x1,x2是方程的两根,且满足(x1-1)(x2-1)=k2-k,求k的值.
分析 (1)根据跟的判别式△=b2-4ac来确定方程的根的情况;
(2)由根与系数的关系x1+x2=-$\frac{b}{a}$、x1x2=$\frac{c}{a}$,代入得出关于k的方程,解方程来求k的值.
解答 解:(1)△=k2-4×1×(-2)=k2+8,
∵k2≥0,
∴k2+8>0,即△>0,
∴无论k为何值,方程总有两个不相等的实数根.
(2)∵设x1,x2是方程x2+kx-2=0的两根,
∴x1+x2=-k,x1x2=-2,
∴(x1-1)(x2-1)=x1x2-(x1+x2)+1=-2+k+1=k2-k
解得:k1=k2=1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.以及根与系数的关系.

练习册系列答案
相关题目
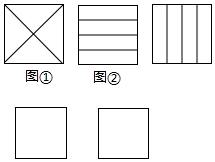 一块正方形空地按下列要求分成四块:(1)被画分割线后整个图形仍是轴对称图形;(2)四个图形形状相同;(3)四个图形面积相等.
一块正方形空地按下列要求分成四块:(1)被画分割线后整个图形仍是轴对称图形;(2)四个图形形状相同;(3)四个图形面积相等.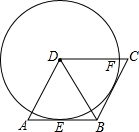 如图,在菱形ABCD中,以点D为圆心的⊙D与AB相切于点E,与DC相交于点F.求证:⊙D与BC也相切.
如图,在菱形ABCD中,以点D为圆心的⊙D与AB相切于点E,与DC相交于点F.求证:⊙D与BC也相切.