题目内容
8.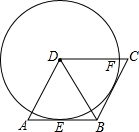 如图,在菱形ABCD中,以点D为圆心的⊙D与AB相切于点E,与DC相交于点F.求证:⊙D与BC也相切.
如图,在菱形ABCD中,以点D为圆心的⊙D与AB相切于点E,与DC相交于点F.求证:⊙D与BC也相切.
分析 作DG⊥BC于G,连结DE,如图,根据切线的性质得DE⊥AB,再根据菱形的性质得BD平分∠ADC,则根据角平分线的性质得DG=DE,然后根据切线的判断定理即可得到⊙D与边BC也相切.
解答  证明:作DG⊥BC于G,连结DE,如图,
证明:作DG⊥BC于G,连结DE,如图,
∵AB与⊙D相切于点E,
∴DE⊥AB,
∵四边形ABCD为菱形,
∴BD平分∠ADC,
而DE⊥AB,DG⊥BC,
∴DG=DE,
即DG为⊙D的半径
∴⊙D与边BC也相切.
点评 本题主要考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线,作出恰当的辅助线是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.用下列哪种方法解方程3(x-2)2=2x-4比较简便( )
| A. | 直接开平方法 | B. | 配方法 | C. | 公式法 | D. | 因式分解法 |





 如图,点D在AE上,BD=CD,∠BDE=∠CDE.求证:AB=AC.
如图,点D在AE上,BD=CD,∠BDE=∠CDE.求证:AB=AC.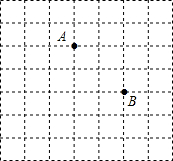 在某旅游景点,为了增加旅游的乐趣,特安排了一次“寻宝”游戏,寻宝人找到了如图所示的两个标志点A(2,1),B(4,-1),这两个标志点到“宝藏”点的距离都是$\sqrt{10}$,请你想想办法,在如图的方格纸中画出这个平面直角坐标系,并求出“宝藏”所在位置的坐标.
在某旅游景点,为了增加旅游的乐趣,特安排了一次“寻宝”游戏,寻宝人找到了如图所示的两个标志点A(2,1),B(4,-1),这两个标志点到“宝藏”点的距离都是$\sqrt{10}$,请你想想办法,在如图的方格纸中画出这个平面直角坐标系,并求出“宝藏”所在位置的坐标.