题目内容
14．已知不等式组$\left\{\begin{array}{l}x＞-1\\ x＜1\\ x＜1-k\end{array}\right.$（1）当k=-2时，不等式组的解集是：-1＜x＜1；当k=3时，不等式组的解集是：无解
（2）由（1）可知，不等式组的解集随k的值变化而变化，若不等式组有解，求k的取值范围并求出解集？
分析 （1）把k=-2和k=3分别代入已知不等式组，分别求得三个不等式的解集，取其交集即为该不等式组的解集；
（2）当k为任意有理数时，要分1-k＜-1，1-k＞1，-1＜1-k＜1三种情况分别求出不等式组的解集．
解答 解：（1）把k=-2代入，得
$\left\{\begin{array}{l}{x＞-1}\\{x＜1}\\{x＜3}\end{array}\right.$，
解得-1＜x＜1；
把k=-3代入，得
$\left\{\begin{array}{l}{x＞-1}\\{x＜1}\\{x＜-2}\end{array}\right.$，
无解．
故答案是：-1＜x＜1；无解；
（2）若k为任意实数，不等式组的解集分以下三种情况：
当1-k≤-1即k≥2时，原不等式组可化为$\left\{\begin{array}{l}{x＞-1\\}\\{x＜-1}\end{array}\right.$，故原不等式组的解集为无解；
当1-k≥1即k≤0时，原不等式组可化为$\left\{\begin{array}{l}{x＞-1}\\{x＜1}\end{array}\right.$，故原不等式组的解集为-1＜x＜1；
当-1＜1-k＜1即0＜k＜2时，原不等式组可化为$\left\{\begin{array}{l}{x＞-1}\\{x＜1-k}\end{array}\right.$，故原不等式组的解集为-1＜x＜1-k．
点评 本题考查的是不等式的解集，特别注意在解（2）时要分三种情况求不等式组的解集．
练习册系列答案
相关题目
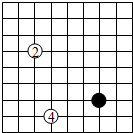如图，围棋棋盘放置在某个平面直角坐标系内，白棋②的坐标为（-7，-4），白棋④的坐标为（-6，-8），那么黑棋的坐标应该是（-3，-7）．
