题目内容
4. 如图,OP为∠AOB内一条射线,C、D分别为OA、OB上两点,且∠PCO+∠PDO=180°,PC=PD.求证:OP平分∠A0B.
如图,OP为∠AOB内一条射线,C、D分别为OA、OB上两点,且∠PCO+∠PDO=180°,PC=PD.求证:OP平分∠A0B.
分析 如图,作辅助线,证明△PMC≌△PND,得到PM=PN,即可解决问题.
解答 证明:如图,过点P作PM⊥OA,PN⊥OB;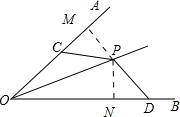
∵∠PCO+∠PDO=180°,∠PCO+∠PCM=180°
∴∠PCM=∠PDN;
在△PMC与△PND中,
$\left\{\begin{array}{l}{∠PMC=∠PND=90°}\\{∠PCM=∠PDN}\\{PC=PD}\end{array}\right.$,
∴△PMC≌△PND(AAS),
∴PM=PN;
∵PM⊥OA,PN⊥OB,
∴OP平分∠A0B.
点评 该题主要考查了角平分线的性质、全等三角形的判定及其性质等几何知识点的应用问题;解题的关键是作辅助线;牢固掌握定理是灵活运用、解题的基础和关键.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
14.下列一元一次方程中,解为x=1的是( )
| A. | 4x-1=3x | B. | 2x-2=3x+3 | C. | 3x+2=2x-1 | D. | 4x-3=3x-1 |
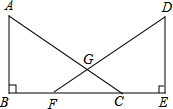 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:AB=DE.
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:AB=DE.
 如图所示,在直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(2,3),B(5,4),C(8,2),试确定这个四边形的面积.
如图所示,在直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(2,3),B(5,4),C(8,2),试确定这个四边形的面积.