题目内容
14.如图①,D是等边△ABC边BA上一动点(点D与点B不重舍),连接DC,以DC为边在BC上方作等边△DCF.连接AF,你能发现线段AF与BD之间的数量关系吗?并证明你发观的结论.如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同.猜想AF与BD在(1)中的结论是否仍然成立?
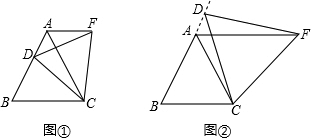
分析 图①,首先根据等边三角形的性质可得AC=BC,∠ACB=60°,DC=CF,∠DCF=60°,再根据等式的性质可得∠DCB=∠ACF,然后证明△BCD≌△FCA可得AF=BD;图②证法与①类似.
解答 解:图①中:AF=BD,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵△DCF是等边三角形,
∴DC=CF,∠DCF=60°,
∴∠ACB-∠DCA=∠DCF-∠DCA,
即∠DCB=∠ACF,
在△BDC和△AFC中$\left\{\begin{array}{l}{AC=BC}\\{∠BCD=∠ACF}\\{DC=FC}\end{array}\right.$,
∴△BCD≌△FCA(SAS),
∴AF=BD;
图②中:AF=BD,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵△DCF是等边三角形,
∴DC=CF,∠DCF=60°,
∴∠ACB+∠DCA=∠DCF+∠DCA,
即∠DCB=∠ACF,
在△BDC和△AFC中$\left\{\begin{array}{l}{AC=BC}\\{∠BCD=∠ACF}\\{DC=FC}\end{array}\right.$,
∴△BCD≌△FCA(SAS),
∴AF=BD.
点评 此题主要考查了全等三角形的判定和性质,以及等边三角形的性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
2. 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I切AC、BC于E、F,射线BI、AI交直线EF于点M、N,设S△AIB=S1,S△MIN=S2,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
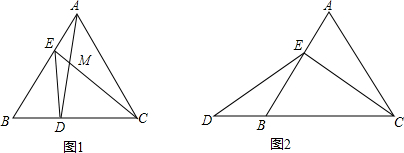
 将一张长方形纸片折叠后如图,若∠2=45°,则∠1,∠3,∠4的度数是多少?
将一张长方形纸片折叠后如图,若∠2=45°,则∠1,∠3,∠4的度数是多少?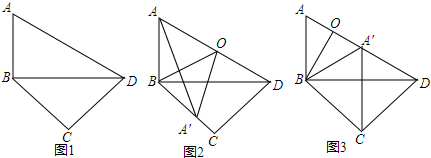
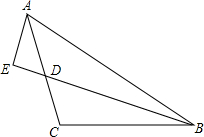 如图,在△ABC中,AC=BC,∠ABC=90°,D是AC的中点,且AE=$\frac{1}{2}$BD,求证:BE是∠ABC的角平分线.
如图,在△ABC中,AC=BC,∠ABC=90°,D是AC的中点,且AE=$\frac{1}{2}$BD,求证:BE是∠ABC的角平分线.