题目内容
16.现场学习题问题背景:
在△ABC中,AB、BC、AC三边的长分别为$\sqrt{2}$、$\sqrt{13}$、$\sqrt{17}$,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
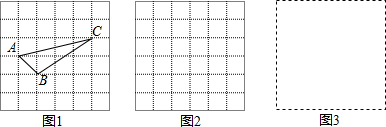
(1)请你将△ABC的面积直接填写在横线上.2.5.
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法,若△ABC三边的长分别为$\sqrt{2}$a,2$\sqrt{5}$a、$\sqrt{26}$a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是:3a2.
探索创新:
(3)若△ABC三边的长分别为$\sqrt{4{m}^{2}+{n}^{2}}$、$\sqrt{16{m}^{2}+{n}^{2}}$、2$\sqrt{{m}^{2}+{n}^{2}}$(m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为:3mn.
分析 (1)把△ABC所在长方形画出来,再用矩形的面积减去周围多余三角形的面积即可;
(2)$\sqrt{2}$a是直角边长为a、a的直角三角形的斜边;2 $\sqrt{5}$a是直角边长为4a,2a的直角三角形的斜边;$\sqrt{26}$a是直角边长为a,5a的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
(3)结合(1),(2)易得此三角形的三边分别是直角边长为n,4m的直角三角形的斜边;直角边长为2m,2n的直角三角形的斜边;直角边长为2m,n的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.
解答 解:(1)S△ABC=4×2-$\frac{1}{2}$×4×1-$\frac{1}{2}$×1×1-$\frac{1}{2}$×2×3=2.5,
故答案为:2.5;
(2)如图所示: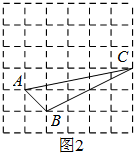
S△ABC=5a×2a-$\frac{1}{2}$×a×a-$\frac{1}{2}$×2a×4a-$\frac{1}{2}$×a×5a=3a2,
故答案为:3a2;
(3)如图所示: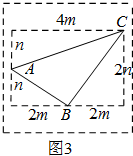
S△ABC=4m×2n-$\frac{1}{2}$×2m×2n-$\frac{1}{2}$×2m×n-$\frac{1}{2}$×4m×n=3mn,
故答案为:3mn.
点评 此题主要考查了勾股定理,作图,本题是开放性的探索问题,关键是结合网格用矩形面积减直角三角形表示出所求三角形的面积.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
11.下列式子中是二次根式的是( )
| A. | $\sqrt{7}$ | B. | $\root{3}{7}$ | C. | $\sqrt{x}$ | D. | $\sqrt{-7}$ |
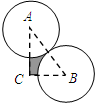 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,分别以A、B为圆心,以$\frac{AB}{2}$为半径作圆,将Rt△ABC截去两个扇形,则剩余部分(阴影)的面积为24-$\frac{25}{4}$πcm2(结果保留π).
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,分别以A、B为圆心,以$\frac{AB}{2}$为半径作圆,将Rt△ABC截去两个扇形,则剩余部分(阴影)的面积为24-$\frac{25}{4}$πcm2(结果保留π).