题目内容
7.若不等式组$\left\{\begin{array}{l}{2x+10<5x-2}\\{3x>2m+1}\end{array}\right.$的解集是x>4,则m的取值范围是m≤$\frac{11}{2}$.分析 首先解第一个不等式,然后根据不等式组的解集是x>4,据此即可求得m的范围.
解答 解:$\left\{\begin{array}{l}{2x+10<5x-2①}\\{3x>2m+1②}\end{array}\right.$,
解①得:x>4,
解②得:x>$\frac{2m+1}{3}$,
∵不等式组$\left\{\begin{array}{l}{2x+10<5x-2}\\{3x>2m+1}\end{array}\right.$的解集是x>4,
∴$\frac{2m+1}{3}$≤4,
解得m≤$\frac{11}{2}$.
故答案是:m≤$\frac{11}{2}$.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
相关题目
17.已知a<b,则有以下结论①a+c<b+c;②$\frac{a}{c}$<$\frac{b}{c}$;③c-a>c-b;④a|c|<b|c|,其中正确的结论个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.在△ABC中,点D、E分别在AB、AC边上,∠B=∠AED,那么下列结论中不正确的是( )
| A. | AD:AC=AE:AB | B. | AD•AB=AE•AC | C. | DE:BC=AD:AC | D. | DE:BC=AD:AB |
19.已知(1,y1),(-3,y2),(-4,y3)是抛物线y=-2x2-8x+m上的点,则( )
| A. | y1<y2<y3 | B. | y2>y1>y3 | C. | y3<y2<y1 | D. | y2>y3>y1 |
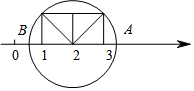 如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画圆,与数轴相交.则圆与数轴的交点所表示的数是2+$\sqrt{2}$或2-$\sqrt{2}$.
如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画圆,与数轴相交.则圆与数轴的交点所表示的数是2+$\sqrt{2}$或2-$\sqrt{2}$.