题目内容
17.已知a<b,则有以下结论①a+c<b+c;②$\frac{a}{c}$<$\frac{b}{c}$;③c-a>c-b;④a|c|<b|c|,其中正确的结论个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据不等式的性质,可得答案.
解答 解:①a+c<b+c,故①符合题意;
②c<0时,$\frac{a}{c}$>$\frac{b}{c}$,故②不符合题意;
③c-a>c-b,两边都乘以-1,不等号的方向改变,故③符合题意;
④c=0时,a|c|=b|c|,故④不符合题意;
故选:A.
点评 本题考查了不等式的性质,熟记不等式的性质是解题关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
2.如果点M在直线y=$\frac{1}{2}$x-3上,则M点的坐标可以是( )
| A. | (-2,-4) | B. | (-2,-3) | C. | (-2,-2) | D. | (-2,-5) |
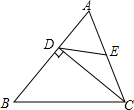 如图,△ABC中,CD⊥AB于点D,若AD=6,DE=5,AC=2DE,则CD的长等于8.
如图,△ABC中,CD⊥AB于点D,若AD=6,DE=5,AC=2DE,则CD的长等于8.