题目内容
3.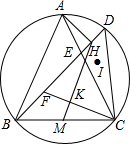 如图,D是△ABC的外接圆上的一点,AB=AC,M是BC的中点,AC与BD交于E,I是△EDC的角平分线的交点,△EIC的外接圆与BD交于点F,AH⊥BD于点H,连接CF,MH.
如图,D是△ABC的外接圆上的一点,AB=AC,M是BC的中点,AC与BD交于E,I是△EDC的角平分线的交点,△EIC的外接圆与BD交于点F,AH⊥BD于点H,连接CF,MH.求证:FC⊥MH.
分析 如图,延长AM交△ABC的外接圆于N,连接ID、IF、IC、EI、DN.首先证明D、I、N共线,HM∥DN,再证明DN⊥CF即可解决问题.
解答 证明:如图,延长AM交△ABC的外接圆于N,连接ID、IF、IC、EI、DN.
∵AB=AC,BM=CM,
∴∠NAB=∠NAC,AM⊥BC,
∴$\widehat{BN}$=$\widehat{CN}$,
∴∠BDN=∠CDN,
∵∠IDE=∠IDC,
∴D、I、N共线,
∵AH⊥BD,
∴∠AHB=∠AMB=90°,
∴A、B、M、H四点共圆,
∴∠BAM=∠BHM,
∵∠BAN=∠BDN,
∴∠BHM=∠BDN,
∴HM∥DN,
∵∠EFI=∠ECI=∠ICD,∠IDF=∠IDC,
在△IDF和△IDC中,
$\left\{\begin{array}{l}{∠IDF=∠IDC}\\{∠IFD=∠ICD}\\{DI=DI}\end{array}\right.$,
∴△IDF≌△IDC,
∴△IDF≌△IDC,
∴IF=IC,DF=DC,
∴DN⊥CF,∵HM⊥DN,
∴HM⊥CF.
点评 本题考查三角形外接圆与外心、三角形的内接圆与内心、等腰三角形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加辅助线构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
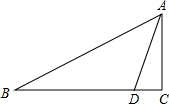 如图,在△ABC中,∠C=90°,D是BC边上一点,∠BAD=45°,AC=3,BD=5,求AB的长.
如图,在△ABC中,∠C=90°,D是BC边上一点,∠BAD=45°,AC=3,BD=5,求AB的长. 如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠3=180°,其中能判断a∥b的是①③④(填序号).
如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠3=180°,其中能判断a∥b的是①③④(填序号).