题目内容
18.求4x2+y2-2y-4x+15的最小值.分析 先将原式变形,化成两个完全平方,再根据完全平方的非负性得最小值.
解答 解:4x2+y2-2y-4x+15,
=4x2-4x+1+y2-2y+1+13,
=(2x-1)2+(y-1)2+13,
因为(2x-1)2≥0,(y-1)2≥0,
所以4x2+y2-2y-4x+15的最小值是13.
点评 本题是配方法的应用,关键是完全平方式的理解与掌握;配方法经常运用于解一元二次方程中,还运用于代数式的求最值问题上,根据完全平方数≥0这一结论,得出相应结果.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
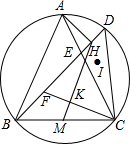 如图,D是△ABC的外接圆上的一点,AB=AC,M是BC的中点,AC与BD交于E,I是△EDC的角平分线的交点,△EIC的外接圆与BD交于点F,AH⊥BD于点H,连接CF,MH.
如图,D是△ABC的外接圆上的一点,AB=AC,M是BC的中点,AC与BD交于E,I是△EDC的角平分线的交点,△EIC的外接圆与BD交于点F,AH⊥BD于点H,连接CF,MH.