题目内容
19.设方程甲:x2-2x-m=0无实根,则判断方程乙:x2+2mx+1+2(m2-1)(x2+1)=0的根的情况是无实数根.分析 首先根据已知方程无实数根,得△<0,求得m的取值范围,再进一步求出新的方程中△的值,与0比较即可.
解答 解:∵x2-2x-m=0无实根,
∴△=4+4m<0,
即m<-1.
将方程x2+2mx+1+2(m2-1)(x2+1)=0化为一般形式是:(2m2-1)x2+2mx+2m2-1=0,
∵m<-1,
∴2m2-1≠0,
∵△=4m2-4(2m2-1)2=4(m+2m2-1)(m-2m2+1)=4(m+1)(2m-1)(-m+1)(2m+1),
∴m+1<0,-m+1>0,2m-1<0,2m+1<0,
∴△<0,
∴该方程无实数根.
故答案为无实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
9.下列命题中,假命题是( )
| A. | 一组邻边相等的矩形是正方形 | |
| B. | 一组邻边相等的平行四边形是菱形 | |
| C. | 对角线互相平分的四边形是平行四边形 | |
| D. | 有一个角是直角的四边形是矩形 |
7.若代数式$\frac{{\sqrt{5x-3}}}{5}$在实数范围内有意义,则x的取值范围是( )
| A. | x>$\frac{3}{5}$ | B. | x<$\frac{3}{5}$ | C. | x≥$\frac{3}{5}$ | D. | x≤$\frac{3}{5}$ |
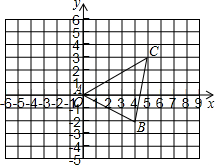 如图A、B、C是△ABC三个顶点
如图A、B、C是△ABC三个顶点