题目内容
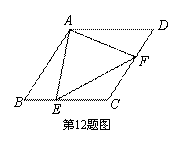
如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若BC= ,求AB的长.
,求AB的长.
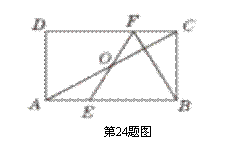
(1)证明:∵ 四边形ABCD是矩形,∴ AB∥CD.
∴ ∠OAE=∠OCF.
又∵ OA=OC, ∠AOE=∠COF,∴ △AEO≌△CFO(ASA).∴ OE=OF.
(2)解:连接BO.∵ BE=BF,∴ △BEF是等腰三角形.
又∵ OE=OF,∴ BO⊥EF,且∠EBO=∠FBO.∴ ∠BOF=90°.
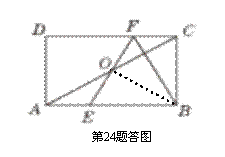
∵ 四边形ABCD是矩形,∴ ∠BCF=90°.
又∵ ∠BEF=2∠BAC,∠BEF=∠BAC+∠EOA,
∴ ∠BAC=∠EOA.∴ AE=OE.
∵ AE=CF,OE=OF,∴ OF=CF.
又∵ BF=BF,∴ Rt△BOF≌Rt△BCF(HL).
∴ ∠OBF=∠CBF.∴ ∠CBF=∠FBO=∠OBE.
∵ ∠ABC=90°,∴ ∠OBE=30°.∴ ∠BEO=60°.∴ ∠BAC=30°.
在Rt△BAC中,∵ BC=2 ,∴ AC=2BC=4
,∴ AC=2BC=4 .
.
AB=
点拨:证明线段相等的常用方法有以下几种:①等腰三角形中的等角对等边;②全等三角形中的对应边相等;③线段垂直平分线的性质;④角平分线的性质;⑤勾股定理;⑥借助第三条线段进行等量代换.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 的算术平方根是( )
的算术平方根是( )
|
| A. | 2 | B. | ±2 | C. |
| D. | ± |

 +(2m
+(2m 1)x+4=0有两个相等的实数根,求m的值.
1)x+4=0有两个相等的实数根,求m的值.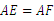 ;
; 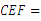 ∠
∠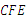 ;
; 
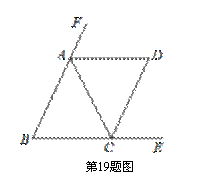
 于点E,作AF⊥直线CD于点F,若AB=10,BC=12,则CE+CF的值为…………………………………………( )
于点E,作AF⊥直线CD于点F,若AB=10,BC=12,则CE+CF的值为…………………………………………( )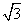 B. 22-11
B. 22-11 ,
, 