题目内容
[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”[1,m-2]的一次函数是正比例函数,解关于x的方程
+
=1.
| 1 |
| x-1 |
| 1 |
| m |
考点:解分式方程,正比例函数的定义
专题:计算题
分析:根据题中新定义求出m的值,代入方程计算即可求出解.
解答:解:∵“关联数”[1,m-2]的一次函数是正比例函数,
∴y=x+m-2为正比例函数,即m-2=0,
解得:m=2,
将m=2代入方程得:
+
=1,
去分母得:2+x-1=2x-2,
移项合并得:x=3,
经检验x=3是分式方程的解.
∴y=x+m-2为正比例函数,即m-2=0,
解得:m=2,
将m=2代入方程得:
| 1 |
| x-1 |
| 1 |
| 2 |
去分母得:2+x-1=2x-2,
移项合并得:x=3,
经检验x=3是分式方程的解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
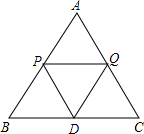 如图,正三角形ABC中,P、Q分别为AB、AC边上的点,将△ABC沿PQ折叠,点A的对称点是点D,小明在研究此折叠问题时,发现一个有趣的结论:不论如何折叠,直线PD和直线BC所成的角总是等于DQ和AC所成的角.如图,点D恰好落在边BC上,试证明∠BDP=∠CQD.
如图,正三角形ABC中,P、Q分别为AB、AC边上的点,将△ABC沿PQ折叠,点A的对称点是点D,小明在研究此折叠问题时,发现一个有趣的结论:不论如何折叠,直线PD和直线BC所成的角总是等于DQ和AC所成的角.如图,点D恰好落在边BC上,试证明∠BDP=∠CQD.