题目内容
15．（1）计算：（x-y）2-（y+2x）（y-2x）；（2）解方程：$\frac{5}{{x}^{2}+3x}$-$\frac{1}{{x}^{2}-x}$=0．
分析 （1）原式利用完全平方公式及平方差公式计算即可得到结果；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）原式=x2-2xy+y2-y2+4x2=5x2-2xy；
（2）去分母得：5（x-1）-（x+3）=0，
去括号得：5x-5-x-3=0，
解得：x=2，
经检验x=2是分式方程的解．
点评 此题考查了解分式方程，完全平方公式，以及平方差公式，熟练掌握公式及运算法则是解本题的关键．
练习册系列答案
目标测试系列答案
相关题目
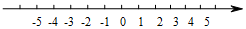在数轴上表示下列各数，并用“＜”连接起来．
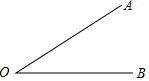已知：∠AOB，如图，利用尺规作∠CDE，使∠CDE=∠AOB．