题目内容
8.已知直线l:y=kx(k<0),将直线y=kx沿y轴向下平移m(m>0)个单位得到直线y=kx-m,平移后的直线与抛物线y=ax2相交于A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点P(6,-9).(1)求a的值;
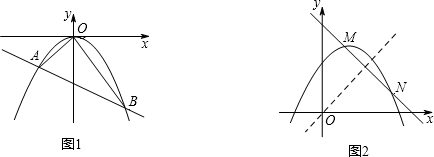
(2)如图1,当∠AOB<90°时,求m的取值范围;
(3)如图2,将抛物线y=ax2向右平移一个单位,再向上平移n个单位(n>0).若第一象限的抛物线上存在点M,N两点,且M,N两点关于直线y=x轴对称,求n的取值范围.
分析 (1)将点P(6,-9)的坐标代入y=ax2,即可求出a的值;
(2)将y=kx-m代入y=-$\frac{1}{4}$x2,得$\frac{1}{4}$x2+kx-m=0,根据二次函数图象上点的坐标特征以及根与系数的关系得出y1=-$\frac{1}{4}$x12,y2=-$\frac{1}{4}$x22,x1•x2=-4m,那么y1•y2=m2.当∠AOB=90°时,如图1,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N.证明△AOM∽△OBN,根据相似三角形对应边成比例得出y1•y2=-x1•x2,依此列出关于m的方程,求出m的值,进而得出当∠AOB<90°时,m的取值范围;
(3)根据轴对称的性质得出直线y=x是线段MN的垂直平分线,如图2,设直线MN的解析式为y=-x+b,与平移后的抛物线y=-$\frac{1}{4}$(x-1)2+n交于M、N两点,交x轴于E点,分别过M,N作y轴、x轴垂线,垂足分别为G、H,设M(m1,n1),N(m2,n2).利用AAS证明△OMG≌△ONH,得出MG=HN,即MG=HE.将y=-$\frac{1}{4}$(x-1)2+n代入y=-x+b得:$\frac{1}{4}$x2-$\frac{3}{2}$x+$\frac{1}{4}$+b-n=0,由根与系数的关系得m1+m2=6,则b=6,那么$\frac{1}{4}$x2-$\frac{3}{2}$x+$\frac{25}{4}$-n=0,再根据△>0以及M,N在第一象限分别列出不等式,进而求出n的取值范围.
解答 解:(1)∵抛物线y=ax2经过点P(6,-9),
∴36a=-9,
解得a=-$\frac{1}{4}$;
(2)将y=kx-m代入y=-$\frac{1}{4}$x2,得$\frac{1}{4}$x2+kx-m=0,
∵y=kx-m与抛物线y=-$\frac{1}{4}$x2相交于A(x1,y1),B(x2,y2)两点,
∴y1=-$\frac{1}{4}$x12,y2=-$\frac{1}{4}$x22,x1•x2=-4m,
∴y1•y2=(-$\frac{1}{4}$x12)•(-$\frac{1}{4}$x22)=$\frac{1}{16}$•(-4m)2=m2.
当∠AOB=90°时,如图1,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N.
在△AOM与△OBN中,
$\left\{\begin{array}{l}{∠OMA=∠BNO=90°}\\{∠OAM=∠BON=90°-∠AOM}\end{array}\right.$,
∴△AOM∽△OBN,
∴$\frac{OM}{BN}$=$\frac{AM}{ON}$,即$\frac{-{x}_{1}}{-{y}_{2}}$=$\frac{-{y}_{1}}{{x}_{2}}$,
∴y1•y2=-x1•x2,
∴m2=4m,
∵m>0,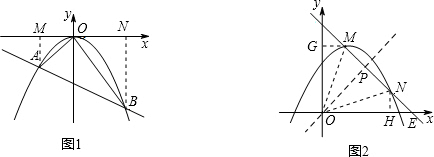 ∴m=4,
∴m=4,
∴当∠AOB<90°时,m>4;
(3)∵M,N两点关于直线y=x轴对称,
∴直线y=x是线段MN的垂直平分线,
∴直线MN的斜率为-1,OM=ON,
∴∠MOP=∠NOP,
∵∠GOP=∠HOP=45°,
∴∠GOM=∠HON.
如图2,设直线MN的解析式为y=-x+b,与平移后的抛物线y=-$\frac{1}{4}$(x-1)2+n交于M、N两点,交x轴于E点.分别过M,N作y轴、x轴垂线,垂足分别为G、H,
设M(m1,n1),N(m2,n2),直线MN与直线y=x交于点P.
在△OMG与△ONH中,
$\left\{\begin{array}{l}{∠GOM=∠HON}\\{∠OGM=∠OHN}\\{OM=ON}\end{array}\right.$,
∴△OMG≌△ONH,
∴MG=HN,即MG=HE.
将y=-$\frac{1}{4}$(x-1)2+n代入y=-x+b得:$\frac{1}{4}$x2-$\frac{3}{2}$x+$\frac{1}{4}$+b-n=0,
由根与系数的关系得m1+m2=6,
∵OE=HE+OH=MG+OH=m1+m2=6,
∴b=6.
即$\frac{1}{4}$x2-$\frac{3}{2}$x+$\frac{25}{4}$-n=0,
∵△>0,
∴(-$\frac{3}{2}$)2-4×$\frac{1}{4}$×($\frac{25}{4}$-n)>0,
解得n>4.
又M,N在第一象限,
∴m1•m2=4($\frac{25}{4}$-n)>0,
解得n<$\frac{25}{4}$,
∴n的取值范围是4<n<$\frac{25}{4}$.
点评 本题是二次函数综合题,考查了待定系数法求抛物线的解析式,二次函数图象上点的坐标特征,根与系数的关系,相似三角形、全等三角形的判定与性质,轴对称的性质,互相垂直的两直线斜率之积为-1的性质,解析式平移的规律,根的判别式等知识,综合性较强,有一定难度.利用数形结合、准确作出辅助线是解题的关键.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 如图,两个反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(其中k1>k2>0)在第一象限内的图象依次是Cl和C2,设点P在C1上,PC⊥x轴于点C,交C1于点A,PD上y轴于点D,交C2于点B,则四边形PAOB的面积为( )
如图,两个反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$(其中k1>k2>0)在第一象限内的图象依次是Cl和C2,设点P在C1上,PC⊥x轴于点C,交C1于点A,PD上y轴于点D,交C2于点B,则四边形PAOB的面积为( )| A. | kl+k2 | B. | kl-k2 | C. | kl•k2 | D. | $\frac{{k}_{1}}{{k}_{2}}$ |
| A. | 地球围绕太阳转 | |
| B. | 早上太阳从西方升起 | |
| C. | 一觉醒来,天气晴朗 | |
| D. | 口袋中有8个白球,从口袋中任取一球,会摸到黑球 |
 如图,△ABC绕旋转中心(-1,0)旋转180°得到△A′B′C′,如果△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
如图,△ABC绕旋转中心(-1,0)旋转180°得到△A′B′C′,如果△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )| A. | (a-2,b) | B. | (a+2,b) | C. | (-a-2,-b) | D. | (a+2,-b) |
| 每户节水量(单位:吨) | 1 | 1.2 | 1.5 |
| 节水户数 | 52 | 30 | 18 |
| A. | 1.20t | B. | 1.15t | C. | 1.05t | D. | 1t |
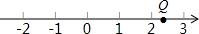 如图,数轴上的点Q所表示的数可能是( )
如图,数轴上的点Q所表示的数可能是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
| A. | 6 | B. | 6π | C. | 12 | D. | 12π |
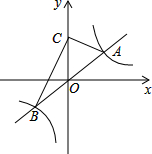 如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=$\frac{3}{4}$x的图象交于A、B两点(点A在第一象限).
如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=$\frac{3}{4}$x的图象交于A、B两点(点A在第一象限).