题目内容
18．
如图，两个反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$（其中k1＞k2＞0）在第一象限内的图象依次是Cl和C2，设点P在C1上，PC⊥x轴于点C，交C1于点A，PD上y轴于点D，交C2于点B，则四边形PAOB的面积为（ ）| A． | kl+k2 | B． | kl-k2 | C． | kl•k2 | D． | $\frac{{k}_{1}}{{k}_{2}}$ |
分析 四边形PAOB的面积为矩形OCPD的面积减去三角形ODB与三角形OAC的面积，根据反比例函数y=$\frac{k}{x}$中k的几何意义，其面积为k1-k2．
解答 解：根据题意可得四边形PAOB的面积=S矩形OCPD-SOBD-SOAC，
由反比例函数y=$\frac{k}{x}$中k的几何意义，可知其面积为k1-k2．
故选B．
点评 主要考查了反比例函数主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点．．
练习册系列答案
相关题目
8．为了建设节约型社会，鼓励居民节约用水，志愿小组在社区宣传时，随机对该社区10户居民的月用水量进行了调查，下表是这10户居民2016年4月份用水量的调查结果：
则这10户居民用水量的中位数为（ ）
| 居民户数 | 1 | 5 | 3 | 1 |
| 月用水量（米3/户） | 10 | 15 | 20 | 25 |
| A． | 15 | B． | 17.5 | C． | 20 | D． | 20 |
尺规作图：（不写作法，保留作图痕迹）
6．圆锥的底面半径为4，母线长为10，则该圆锥的侧面积为（ ）
| A． | 80π | B． | 40π | C． | 20π | D． | 10π |
13．小华是9人队伍中的一员，他们随机排成一列队伍，从1开始按顺序报数，小华报到偶数的概率是（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{4}{9}$ | C． | $\frac{1}{2}$ | D． | $\frac{5}{9}$ |
3．
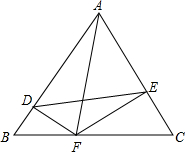△ABC为等边三角形，边长为a，DF⊥AB．EF⊥AC
（1）求证：△BDF∽△CEF；
（2）若a=4，设BF=m，四边形ADFE面积为S，求出S与m之间的函数关系式，并探究当m为何值时S取最大值．
△ABC为等边三角形，边长为a，DF⊥AB．EF⊥AC（1）求证：△BDF∽△CEF；
（2）若a=4，设BF=m，四边形ADFE面积为S，求出S与m之间的函数关系式，并探究当m为何值时S取最大值．
10．用配方法解方程x2-1=6x，配方后的方程是（ ）
| A． | （x-3）2=9 | B． | （x-3）2=1 | C． | （x-3）2=10 | D． | （x+3）2=9 |
7．
一个几何体的三视图如图所示，那么这个几何体是（ ）
一个几何体的三视图如图所示，那么这个几何体是（ ）| A． |  | B． |  | C． |  | D． |  |
