题目内容
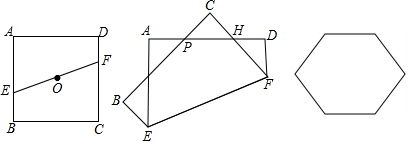
9. 如图,菱形ABCD的周长为40,面积为25,P是对角线BC上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于2.5.
如图,菱形ABCD的周长为40,面积为25,P是对角线BC上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于2.5.
分析 直接利用菱形的性质得出AB=AD=10,S△ABD=12.5,进而利用三角形面积求法得出答案.
解答 解:∵菱形ABCD的周长为40,面积为25,
∴AB=AD=10,S△ABD=12.5,
∵分别作P点到直线AB、AD的垂线段PE、PF,
∴$\frac{1}{2}$×AB×PE+$\frac{1}{2}$×PF×AD=12.5,
∴$\frac{1}{2}$×10(PE+PF)=12.5,
∴PE+PF=2.5.
故答案为:2.5.
点评 此题主要考查了菱形的性质,正确得出$\frac{1}{2}$×AB×PE+$\frac{1}{2}$×PF×AD=S△ABD是解题关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
19.若方程组$\left\{\begin{array}{l}{ax+y=5}\\{x+by=-1}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,则点P(a,b)所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.下列调查中,适合普查的事件是( )
| A. | 调查华为手机的使用寿命 | |
| B. | 调查我国七年级学生的心理健康情况 | |
| C. | 调查我班学生身高的情况 | |
| D. | 调查中央电视台《朗读者》节目的收视率 |
4.下列函数中,自变量x的取值范围为x≥3的是( )
| A. | y=$\sqrt{x+3}$ | B. | y=$\sqrt{x-3}$ | C. | y=$\frac{1}{x+3}$ | D. | y=$\frac{1}{x-3}$ |
18.不等式-2x+3≥5的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |