题目内容
20.小明想用边长为6.8厘米正方形纸片折出一个正八边形.通过若干次尝试,他发现当折痕是一条通过正方形的对角线交点O的直线EF时,可得到图2,用剪刀剪去△EBG,△GAP,△PCH,△HDF时,展开纸片就可得到正八边形,求这个正八边形的面积.(参考数值$\sqrt{2}$=1.4,$\sqrt{3}$=1.7)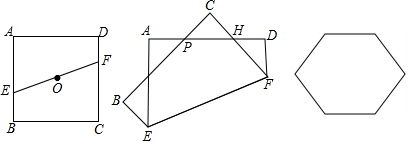
分析 易知△BEG≌△AGP≌△CPH≌△DHF,推出BE=BG=AG=PA=PC=CH=DH=DF,EG=PH=HF,推出S△BEG=S△AGP=S△CPH=S△DHF,设BE=x,则EG=$\sqrt{2}$x,可得2x+$\sqrt{2}$x=6.8,推出x=2,可得S△BEG=$\frac{1}{2}$×2×2=2,根据S八边形=S正方形ABCD-4•S△BEG计算即可.
解答 解:由题意可知△BEG≌△AGP≌△CPH≌△DHF,
∴BE=BG=AG=PA=PC=CH=DH=DF,EG=PH=HF,
∴S△BEG=S△AGP=S△CPH=S△DHF,设BE=x,则EG=$\sqrt{2}$x,
∴2x+$\sqrt{2}$x=6.8,
∴x=2,
∴S△BEG=$\frac{1}{2}$×2×2=2,
∴S八边形=6.82-4×2=38.24.
点评 本题考查剪纸问题,正方形的性质、全等三角形的性质,等腰直角三角形的性质等知识,解题的关键是学会利用参数,构建方程解决问题.

练习册系列答案
相关题目
11.已知两条线段的长分别为$\sqrt{2}$和$\sqrt{7}$,能与它们组成直角三角形的线段长是( )
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{5}$或3 | D. | $\sqrt{5}$或$\sqrt{2}$ |
8.若关于x的不等式组$\left\{\begin{array}{l}{6+2x≥0}\\{x≤m}\end{array}\right.$有解,则m的取值范围是( )
| A. | m<-3 | B. | m≤-3 | C. | m>-3 | D. | m≥-3 |
15.1张新版百元的人民币厚约为0.00009米,数据“0.00009米”用科学记数法可表示为( )
| A. | 9×10-5米 | B. | 9×10-4米 | C. | 0.9×10-6米 | D. | 90×10-3米 |
5.下列四个数中,其中最小的数是( )
| A. | -4 | B. | 0 | C. | -π | D. | $\sqrt{2}$ |
10.下列语句是命题的是( )
| A. | 对角线相等吗? | B. | 作线段AB=10cm | C. | 若a=b,则-a=-b | D. | 连结A、B两点 |
 如图,函数y=2x+b与函数y=kx-1的图象交于点P,那么点P的坐标为(1,-2),关于x的不等式kx-1>2x+b的解集是x<1.
如图,函数y=2x+b与函数y=kx-1的图象交于点P,那么点P的坐标为(1,-2),关于x的不等式kx-1>2x+b的解集是x<1. 如图,菱形ABCD的周长为40,面积为25,P是对角线BC上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于2.5.
如图,菱形ABCD的周长为40,面积为25,P是对角线BC上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于2.5.