题目内容
17.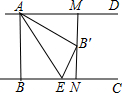 如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M、N,当点MB′=$\frac{1}{3}$MN时,BE的长为$\frac{3\sqrt{2}}{2}$.
如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M、N,当点MB′=$\frac{1}{3}$MN时,BE的长为$\frac{3\sqrt{2}}{2}$.
分析 根据勾股定理,可得EB′,根据相似三角形的性质,可得EN的长,根据勾股定理,可得答案.
解答 解:由翻折的性质,得
AB=AB′,BE=B′E.
∵MB′=$\frac{1}{3}$MN,
∴MB′=1,B′N=2,设EN=x,得
B′E=$\sqrt{{x}^{2}+{2}^{2}}$,
△B′EN∽△AB′M,
∴$\frac{EN}{B′M}$=$\frac{B′E}{AB′}$,即$\frac{x}{1}$=$\frac{\sqrt{{x}^{2}+4}}{3}$,
解得x2=$\frac{1}{2}$,BE=B′E=$\sqrt{\frac{1}{2}+4}$=$\frac{3\sqrt{2}}{2}$,
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查了翻折的性质,利用翻折的性质得出AB=AB′,BE=B′E是解题关键,又利用了相似三角形的性质.

练习册系列答案
相关题目
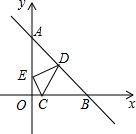 如图,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为($\frac{25}{7}$,$\frac{24}{7}$).
如图,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为($\frac{25}{7}$,$\frac{24}{7}$).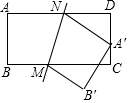 如图,矩形纸片ABCD中,AB=1,BC=2,点M,N分别在边BC,AD上,将纸片ABCD沿直线MN对折,使点A落在CD边上,则线段BM的取值范围是$\frac{3}{4}$≤BM≤1.
如图,矩形纸片ABCD中,AB=1,BC=2,点M,N分别在边BC,AD上,将纸片ABCD沿直线MN对折,使点A落在CD边上,则线段BM的取值范围是$\frac{3}{4}$≤BM≤1.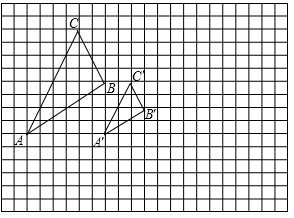 如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,他们的顶点都在小正方形的顶点上.
如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,他们的顶点都在小正方形的顶点上.
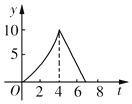
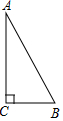 如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,两只小虫(不计大小)分别从C点出发,小虫1沿CA-AB-BC运动,速度大小为2cm/s,小虫2沿CB-BA-AC运动,速度大小为$\frac{3}{2}$cm/s,相遇后停止.这一过程中两小虫之间的距离y与时间t的关系的大致图象是( )
如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,两只小虫(不计大小)分别从C点出发,小虫1沿CA-AB-BC运动,速度大小为2cm/s,小虫2沿CB-BA-AC运动,速度大小为$\frac{3}{2}$cm/s,相遇后停止.这一过程中两小虫之间的距离y与时间t的关系的大致图象是( )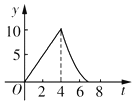
 如图,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是$\sqrt{5}$,则圆锥的母线l=3$\sqrt{5}$.
如图,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面圆半径是$\sqrt{5}$,则圆锥的母线l=3$\sqrt{5}$.