题目内容
8.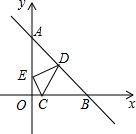 如图,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为($\frac{25}{7}$,$\frac{24}{7}$).
如图,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为($\frac{25}{7}$,$\frac{24}{7}$).
分析 点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″(7,6),连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,可以根据待定系数法求得直线DE的解析式,然后联立方程,求得交点D的坐标.
解答 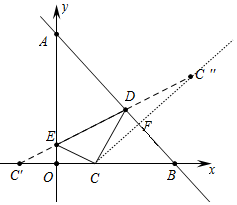 解:如图,点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″,
解:如图,点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″,
∵直线AB的解析式为y=-x+7,
∴直线CC″的解析式为y=x-1,
由$\left\{\begin{array}{l}{y=-x+7}\\{y=x-1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,
∴F(4,3),
∵F是CC″中点,
∴可得C″(7,6).
连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,
∵C′(-1,0),C″(7,6),
∴设直线DE的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-k+b=0}\\{7k+b=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=\frac{3}{4}}\end{array}\right.$,
∴直线DE的解析式为y=$\frac{3}{4}$x+$\frac{3}{4}$,
由$\left\{\begin{array}{l}{y=-x+7}\\{y=\frac{3}{4}x+\frac{3}{4}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{25}{7}}\\{y=\frac{24}{7}}\end{array}\right.$,
∴点D坐标为($\frac{25}{7}$,$\frac{24}{7}$),
故答案为($\frac{25}{7}$,$\frac{24}{7}$).
点评 本题考查轴对称-最短问题、待定系数法求一次函数的解析式以及直线的交点问题,解题的关键是利用对称性在找到点D、点E位置,属于中考常考题型.

为调查不同品牌饮料的市场销售情况,小东和小芸两位同学对一家超市进行了调查,二人在某天对照50名顾客购买饮料的品牌进行了记录.
小东的作法是:如果一个顾客购买某一品牌的饮料,就将这一饮料的品牌名字记录一次.表1是记录的初始数据.
表1
| 统一冰茶 | 可口可乐 | 统一冰茶 | 汇源果汁 | 露露 |
| 露露 | 统一冰茶 | 可口可乐 | 露露 | 可口可乐 |
| 统一冰茶 | 可口可乐 | 可口可乐 | 百事可乐 | 统一冰茶 |
| 可口可乐 | 百事可乐 | 统一冰茶 | 可口可乐 | 百事可乐 |
| 百事可乐 | 露露 | 露露 | 百事可乐 | 露露 |
| 可口可乐 | 统一冰茶 | 统一冰茶 | 汇源果汁 | 汇源果汁 |
| 汇源果汁 | 统一冰茶 | 可口可乐 | 可口可乐 | 可口可乐 |
| 可口可乐 | 百事可乐 | 露露 | 汇源果汁 | 百事可乐 |
| 露露 | 可口可乐 | 百事可乐 | 可口可乐 | 露露 |
| 可口可乐 | 统一冰茶 | 百事可乐 | 汇源果汁 | 统一冰茶 |
表2
| 饮料名称 | 频数 |
| 可口可乐 | 15 |
| 统一冰茶 | 11 |
| 百事可乐 | 9 |
| 露露 | 9 |
| 汇源果汁 | 6 |
| 合计 | 50 |
| 饮料名称 | 画记 | 频数 |
| 可口可乐 | 正正正 | 15 |
| 统一冰茶 | 正正一 | 11 |
| 百事可乐 | 正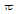 | 9 |
| 露露 | 正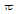 | 9 |
| 汇源果汁 | 正一 | 6 |
| 合计 | 50 |
根据以上材料回答问题:
本次调查如果让你去做,在收集整理数据时,你会选择他们中的哪种方法?请你说明理由或者介绍一种新的方法.
| 家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
| 挂钟 | 30 | 2 | 60 |
| 垃圾桶 | 15 | ||
| 塑料鞋架 | 40 | ||
| 艺术字画 | a | 2 | 90 |
| 电热水壶 | 35 | 1 | b |
| 合计 | 8 | 280 | |
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
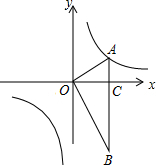 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$(x≠0)的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$(x≠0)的图象上.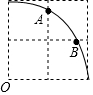 在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧交图中网格线与点A,B,则弧AB的长是$\frac{π}{3}$.
在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧交图中网格线与点A,B,则弧AB的长是$\frac{π}{3}$.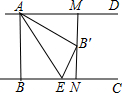 如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M、N,当点MB′=$\frac{1}{3}$MN时,BE的长为$\frac{3\sqrt{2}}{2}$.
如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M、N,当点MB′=$\frac{1}{3}$MN时,BE的长为$\frac{3\sqrt{2}}{2}$.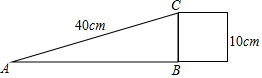 为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )


