题目内容
11.解方程:(1)3x2-5x-2=0
(2)x2-4x-2=0.
分析 (1)方程左边利用十字相乘法分解因式后,利用两数相乘积为0,两因式至少有一个为0转化为两个一元一次方程来求解;
(2)先计算判别式的值,然后利用求根公式解方程.
解答 解:(1)因式分解得:(3x+1)(x-2)=0,
可得3x+1=0或x-2=0,
解得:x1=-$\frac{1}{3}$,x2=2;
(2)△=(-4)2-4×1×(-2)=24,
x=$\frac{4±\sqrt{24}}{2}$,
所以x1=2+$\sqrt{6}$,x2=2-$\sqrt{6}$.
点评 此题考查了解一元二次方程-因式分解法,利用此方法解方程时,首先将方程右边化为0,左边化为积的形式,然后利用两数相乘积为0,两因式至少有一个为0转化为两个一元一次方程来求解.也考查了公式法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列计算正确的是( )
| A. | -1+2=-3 | B. | -1-1=0 | C. | 0-2=2 | D. | -2-(-5)=3 |
3.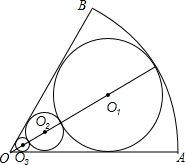 如图所示,扇形AOB中,∠AOB=60°,AO=R,圆O1与AO,BO和弧AB都相切;圆O2和圆O1,AO,BO都相切;圆O3和圆O2;AO,BO都相切;则圆O3的面积为( )
如图所示,扇形AOB中,∠AOB=60°,AO=R,圆O1与AO,BO和弧AB都相切;圆O2和圆O1,AO,BO都相切;圆O3和圆O2;AO,BO都相切;则圆O3的面积为( )
 如图所示,扇形AOB中,∠AOB=60°,AO=R,圆O1与AO,BO和弧AB都相切;圆O2和圆O1,AO,BO都相切;圆O3和圆O2;AO,BO都相切;则圆O3的面积为( )
如图所示,扇形AOB中,∠AOB=60°,AO=R,圆O1与AO,BO和弧AB都相切;圆O2和圆O1,AO,BO都相切;圆O3和圆O2;AO,BO都相切;则圆O3的面积为( )| A. | $\frac{π{R}^{2}}{2187}$ | B. | $\frac{8π{R}^{2}}{2187}$ | C. | $\frac{π{R}^{2}}{729}$ | D. | $\frac{8π{R}^{2}}{729}$ |
1.顺次连接矩形ABCD各边中点得到四边形EFGH,它的形状是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
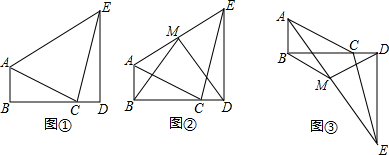
 阅读下列材料,并回答问题.
阅读下列材料,并回答问题.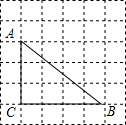 如图,正方形网格的每一个小正方形的边长都为1,△ABC的三个顶点都在正方形的顶点上,完成下面问题:
如图,正方形网格的每一个小正方形的边长都为1,△ABC的三个顶点都在正方形的顶点上,完成下面问题: