题目内容
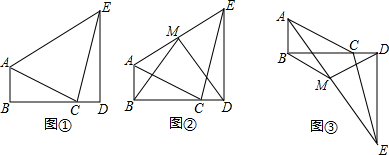
2.已知Rt△ABC≌Rt△CDE;现将它们摆放成图①所示位置,其中B、C、D三点在同一直线上,连接AE.(1)如图①,若AB=2,BC=4,求AE的长;
(2)如图②,取AE的中点M,连接BM、DM,证明:BM=DM;
(3)如图③,将图①的Rt△CDE以直线CD为对称轴向下翻折,仍然连接AE,取AE的中点M,连接BM、DM,请问:BM=DM还成立吗?请说明理由.
分析 (1)根据全等三角形的性质得到∠BAC=∠DCE,AC=CE,利用角与角之间的数量关系以及直角的性质即可证明AC⊥CE,再利用勾股定理即可求出AE的长;
(2)连接CM,证明出△ABM≌△CDM,即可得到BM=DM;
(3)延长BM交DE于点N,利用AAS证明△ABM≌△ENM,于是得到BM=MN,再根据直角三角形的性质可得BM=DM.
解答 解:(1)∵Rt△ABC≌Rt△CDE,
∴∠BAC=∠DCE,AC=CE,
在Rt△ABC中,
∵∠BAC+∠BCA=90°,
∴∠DCE+∠BCA=90°,
∵B,C,D三点共线,
∴∠ACE=180°-(∠DCE+∠BCA)=90°,
∴AC⊥CE,
∴AE2=AC2+CE2,
∵AC2=AB2+BC2,
∴AE=$\sqrt{2}$AC=$\sqrt{2}$×2$\sqrt{5}$=2$\sqrt{10}$;
(2)连接CM,如图②,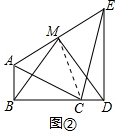
∵△ACE是直角三角形,点M是AE的中点,
∴CM=AM=$\frac{1}{2}$AE,
在△ABM和△CDM中,
$\left\{\begin{array}{l}{AB=CD}\\{∠BAM=∠DCM}\\{AM=CM}\end{array}\right.$,
∴△ABM≌△CDM,
∴BM=DM;
(3)如图③,延长BM交DE于点N,
∵∠ABD=∠CDE=90°,
∴AB∥DE,
∴∠BAM=∠DEM,
在△ABM和△ENM中,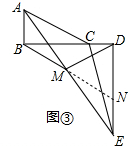
$\left\{\begin{array}{l}{∠BAM=∠DEM}\\{∠AMB=∠NME}\\{AM=EM}\end{array}\right.$,
∴△ABM≌△ENM,
∴BM=MN,
在Rt△BDN中,
∵M是BN的中点,
∴BM=MN=DM=$\frac{1}{2}$BN,
∴BM=DM.
点评 本题主要考查了全等三角形的判定与性质的知识,解答本题的关键是作辅助线构造两个全等的三角形,此题还需要掌握全等三角形的判定定理,此题难度不大.

| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -4 | +7 | -9 | +8 | +6 | -5 | -2 |
(2)在第四次纪录时距A地最远,最远距离是8千米.
(3)若每km耗油0.3升,问共耗油多少升?

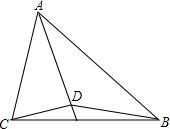 如图所示,在△ABC中,∠BAC=60°,∠B=45°,AD平分∠BAC,AC=10,S△ADC=25,求AB和BD的长.
如图所示,在△ABC中,∠BAC=60°,∠B=45°,AD平分∠BAC,AC=10,S△ADC=25,求AB和BD的长.