题目内容
7. 如图,P是∠α的边OA上一点,且点P的坐标为(1,$\sqrt{7}$),则sinα=$\frac{\sqrt{14}}{4}$.
如图,P是∠α的边OA上一点,且点P的坐标为(1,$\sqrt{7}$),则sinα=$\frac{\sqrt{14}}{4}$.
分析 根据点P坐标和勾股定理得出OP的长,再利用三角函数的定义即可得出sinα.
解答 解:∵点P的坐标为(1,$\sqrt{7}$),
∴OP=$\sqrt{{1}^{2}+(\sqrt{7})^{2}}$=2$\sqrt{2}$,
∴sinα=$\frac{\sqrt{7}}{2\sqrt{2}}$=$\frac{\sqrt{14}}{4}$,
故答案为$\frac{\sqrt{14}}{4}$.
点评 本题考查了解直角三角形以及坐标与图形变换,掌握勾股定理和三角函数的定义是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
18.下列不等式中,正确的个数是( )
-4$\frac{2}{3}$>-4.7,-$\frac{12}{23}$<-$\frac{6}{11}$,-0.$\stackrel{•}{2}$>-0.22,-0.01<-$\frac{1}{100}$.
-4$\frac{2}{3}$>-4.7,-$\frac{12}{23}$<-$\frac{6}{11}$,-0.$\stackrel{•}{2}$>-0.22,-0.01<-$\frac{1}{100}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12. 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
16.若m是任意实数,则点A(m2+1,-4)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
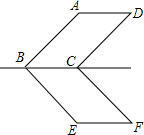 如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F.
如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F. 如图所示,经过圆内一点P作弦AB和CD,且DP=BP,求证:PA=PC.
如图所示,经过圆内一点P作弦AB和CD,且DP=BP,求证:PA=PC. 如图,在5×4的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个3个.
如图,在5×4的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个3个.