题目内容
3.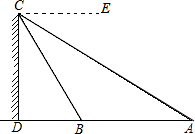 如图,A、B两点与建筑物底部D在同一直线上,从建筑物顶部C点测得∠ECA=30°,∠ECB=60°,且AB=20,求建筑物CD的高.
如图,A、B两点与建筑物底部D在同一直线上,从建筑物顶部C点测得∠ECA=30°,∠ECB=60°,且AB=20,求建筑物CD的高.
分析 根据∠ECA=30°,∠ECB=60°,可得∠ACB、∠A、∠BCD的度数,由AB=20,可得BC的长,从而可以求得CD的长.
解答 解:∵∠ECA=30°,∠ECB=60°,
∴∠ACD=60°,∠ACB=30°.
∴∠BCD=30°,∠A=30°.
∴∠ACB=∠A.
∴AB=CB.
∵AB=20,∠ADC=90°,∠BCD=30°,
∴BC=20,CD=BC•cos30°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$.
即建筑物CD的高为10$\sqrt{3}$.
点评 本题考查解直角三角形,解题的关键是灵活变化,找出所求问题需要的条件.

练习册系列答案
相关题目
14.下面各组线段中,能组成三角形的是( )
| A. | 5,2,3 | B. | 10,5,4 | C. | 4,8,4 | D. | 2,3,4 |