题目内容
15.现有两根木棒的长度分别是400cm和500cm,若要钉成一个三角形木架,其中有一个角为直角,则所需木棒的最短长度为300cm.分析 当斜边为500cm,直角边为400cm时,所需第三根木棒的长度最短,根据勾股定理得出答案即可.
解答 解:现有两根木棒的长度分别是400cm和500cm,若要钉成一个三角形木架,其中有一个角为直角,
当斜边为500cm,直角边为400cm时,所需第三根木棒的长度最短,
此时,木棒的最短长度为$\sqrt{50{0}^{2}-40{0}^{2}}$=300(cm).
故答案为:300cm.
点评 本题主要考查了勾股定理的应用,正确的记忆勾股定理确定好斜边与直角边是解决问题的关键,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.如果m-n=3,mn=1,那么m2+n2的值是( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
10.已知:四边形ABCD是正方形,在平面内找一点P满足△PAB,△PBC,△PCD,△PAD均为等腰三角形,这样的点P有( )个.
| A. | 7个 | B. | 8个 | C. | 9个 | D. | 10个 |
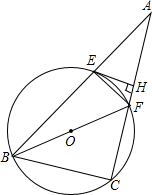 已知:如图,⊙O过△ABC的B、C两点,分别交AB、AC于点E、F.
已知:如图,⊙O过△ABC的B、C两点,分别交AB、AC于点E、F.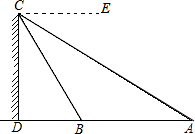 如图,A、B两点与建筑物底部D在同一直线上,从建筑物顶部C点测得∠ECA=30°,∠ECB=60°,且AB=20,求建筑物CD的高.
如图,A、B两点与建筑物底部D在同一直线上,从建筑物顶部C点测得∠ECA=30°,∠ECB=60°,且AB=20,求建筑物CD的高. 小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数共有5个.
小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数共有5个.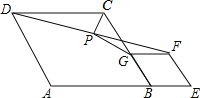 如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则$\frac{CP}{CG}$=$\frac{1}{2}$.
如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则$\frac{CP}{CG}$=$\frac{1}{2}$.