题目内容
13.计算题.(1)$\sqrt{32}-3\sqrt{\frac{1}{2}}+\sqrt{2}$
(2)($\sqrt{\frac{9}{2}}-\frac{\sqrt{98}}{3}$)×$2\sqrt{2}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的乘法运算.
解答 解:(1)原式=4$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$+$\sqrt{2}$
=$\frac{7\sqrt{2}}{2}$;
(2)原式=($\frac{3\sqrt{2}}{2}$-$\frac{7\sqrt{2}}{3}$)×2$\sqrt{2}$
=$\frac{-5\sqrt{2}}{6}$×2$\sqrt{2}$
=-$\frac{10}{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
3.下列说法中正确的是( )
| A. | n没有系数 | B. | b的指数是0 | C. | 0不是单项式 | D. | -x的系数是-1 |
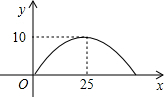 有一个抛物线形拱桥,其最大高度为10m,跨度为50m,现把它的示意图放在平面直角坐标系中,如图所示,则抛物线的函数解析式为y=-$\frac{2}{125}$(x-25)2+10.
有一个抛物线形拱桥,其最大高度为10m,跨度为50m,现把它的示意图放在平面直角坐标系中,如图所示,则抛物线的函数解析式为y=-$\frac{2}{125}$(x-25)2+10.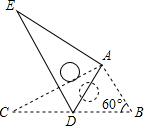 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC=$\sqrt{3}$,∠B=60°,则CD的长为1.
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC=$\sqrt{3}$,∠B=60°,则CD的长为1.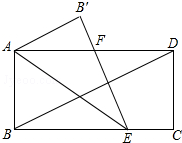 如图,在矩形ABCD中,AD=2AB,将矩形沿AE折叠,使B落到B′的位置,并且B′E与对角线BD垂直.
如图,在矩形ABCD中,AD=2AB,将矩形沿AE折叠,使B落到B′的位置,并且B′E与对角线BD垂直.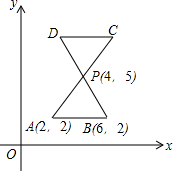 如图,AC与BD交于P点,PA=PB=PC=PD,已知△PAB的三点坐标为A(2,2),B(6,2),P(4,5).
如图,AC与BD交于P点,PA=PB=PC=PD,已知△PAB的三点坐标为A(2,2),B(6,2),P(4,5).